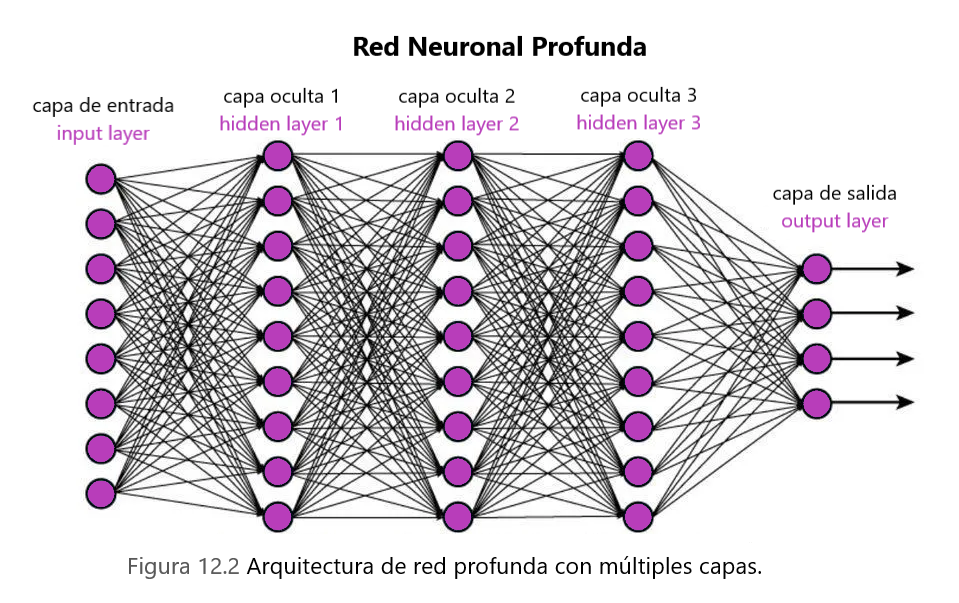
Las redes neuronales profundas son un avance clave en el campo de la visión por computadora y el reconocimiento de voz. Durante la última década, las redes neuronales profundas han permitido a las máquinas reconocer imágenes, voz e incluso jugar con una precisión casi imposible para los humanos.
Para lograr un alto nivel de precisión, se necesita una gran cantidad de datos y, en adelante, potencia informática para entrenar estas redes neuronales profundas.
Sin embargo, a pesar de la complejidad computacional involucrada, podemos seguir ciertas pautas para reducir el tiempo de entrenamiento y mejorar la precisión del modelo. En este artículo veremos algunas de estas técnicas.
Preprocesamiento de datos
La importancia del preprocesamiento de datos sólo puede enfatizarse por el hecho de que su red neuronal es tan buena como los datos de entrada utilizados para entrenarla.
Si faltan entradas de datos importantes, es posible que la red neuronal no pueda alcanzar el nivel de precisión deseado. Por otro lado, si los datos no se procesan de antemano, podría afectar la precisión y el rendimiento de la red en el futuro.
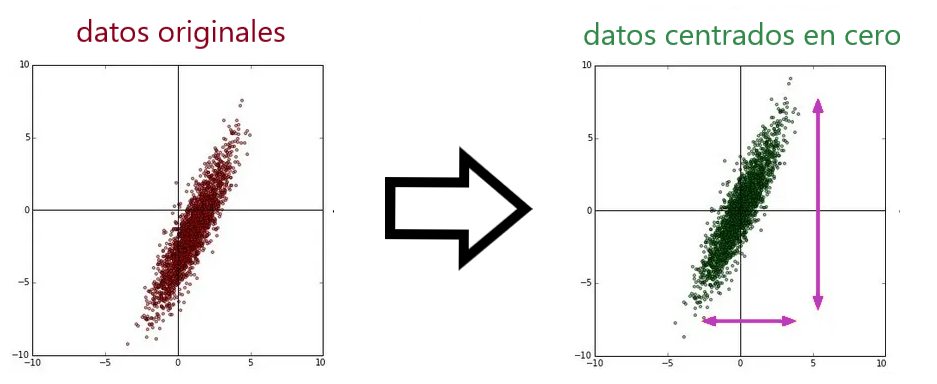
Resta media (centrado en cero)
Es el proceso de restar la media de cada uno de los puntos de datos para centrarlo en cero. Considere un caso en el que las entradas a la neurona (unidad) son todas positivas o todas negativas.
En ese caso, el gradiente calculado durante la retro propagación será positivo o negativo (igual que el signo de las entradas). Y, por lo tanto, las actualizaciones de parámetros solo se restringen a direcciones específicas, lo que a su vez hará que la convergencia sea ineficiente.
Normalización de datos
La normalización se refiere a normalizar los datos para que tengan la misma escala en todas las dimensiones. La forma común de hacerlo es dividir los datos de cada dimensión por su desviación estándar.
Sin embargo, solo tiene sentido si tiene una razón para creer que diferentes características de entrada tienen diferentes escalas pero tienen la misma importancia para el algoritmo de aprendizaje.

Inicialización de parámetros
Las redes neuronales profundas no son ajenas a millones o miles de millones de parámetros. La forma en que se inicializan estos parámetros puede determinar qué tan rápido convergería nuestro algoritmo de aprendizaje y qué tan preciso podría terminar.
La forma más sencilla es inicializarlos todos a cero. Sin embargo, si inicializamos los pesos de una capa a cero, los gradientes calculados serán los mismos para cada unidad de la capa y, por lo tanto, la actualización de los pesos sería la misma para todas las unidades. En consecuencia, esa capa es tan buena como una única unidad de regresión logística.
Seguramente podemos hacerlo mejor inicializando los pesos con algunos números aleatorios pequeños . ¿No es así? Bueno, analicemos la fecundidad de esa hipótesis con una red neuronal profunda de 10 capas, cada una de las cuales consta de 500 unidades y utiliza la función de activación tanh. [Solo una nota sobre la activación de tanh antes de continuar].

A la izquierda está el gráfico de la función de activación tanh. Hay algunos puntos importantes que debemos recordar sobre esta activación a medida que avanzamos: –
- Esta activación está centrada en cero.
- Se satura en caso de que la entrada sea un número positivo grande o un número negativo grande.
Para empezar, inicializamos todos los pesos de un gaussiano estándar con media cero y desviación estándar 1 e-2.
W = 0,01 * np.random.randn(fan_in, fan_out)
Desafortunadamente, esto sólo funciona bien para redes neuronales profundas pequeñas. Y para ver qué problemas crea para redes más profundas, se generan gráficos con varios parámetros. Estos gráficos representan la media, la desviación estándar y la activación de cada capa a medida que profundizamos en la red.
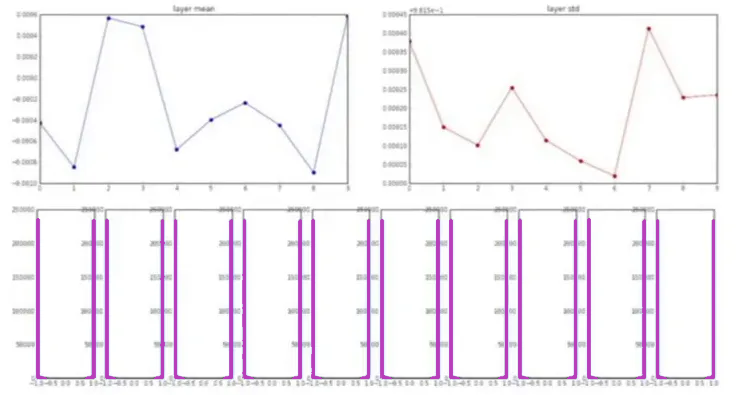

Observe que la media siempre está alrededor de cero, lo cual es obvio ya que estamos usando no linealidad centrada en cero. Sin embargo, la desviación estándar se reduce gradualmente a medida que nos adentramos en la red hasta que colapsa a cero.
Esto también es obvio debido al hecho de que estamos multiplicando las entradas con pesos muy pequeños en cada capa. En consecuencia, los gradientes calculados también serían muy pequeños y, por tanto, la actualización de las ponderaciones será insignificante.
Pues no tan bien!!! A continuación, intentemos inicializar pesos con números muy grandes. Para hacerlo, tomemos una muestra de pesos del gaussiano estándar con media cero y desviación estándar de 1,0 (en lugar de 0,01 ).
W = 1,0 * np.random.randn(fan_in, fan_out)
A continuación se muestran los gráficos que muestran la media, la desviación estándar y la activación de todas las capas.
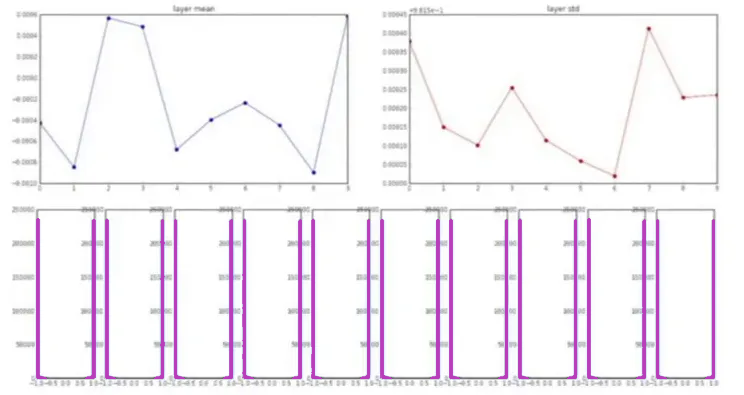
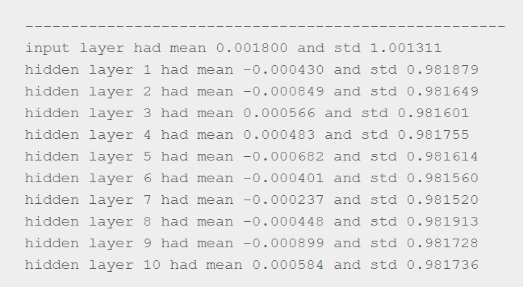
Tenga en cuenta que la activación en cada capa es cercana a 1 o -1, ya que estamos multiplicando las entradas con pesos muy grandes y luego alimentándolas para lograr la no linealidad (se aplasta en el rango de +1 a -1).
En consecuencia, los gradientes calculados también estarían muy cerca de cero a medida que tanh se satura en estos regímenes (la derivada es cero). Finalmente, las actualizaciones del peso volverían a ser casi insignificantes.
En la práctica, la inicialización de Xavier se utiliza para inicializar los pesos de todas las capas. La motivación detrás de la inicialización de Xavier es inicializar los pesos de tal manera que no terminen en regímenes saturados de activación tanh, es decir, inicializar con valores ni demasiado pequeños ni demasiado grandes.
Para lograrlo, escalamos según el número de entradas mientras tomamos un muestreo aleatorio del gaussiano estándar.
W = 1,0 * np.random.randn(fan_in, fan_out) / np.sqrt(fan_in)
Sin embargo, esto funciona bien asumiendo que tanh se usa para la activación. Esto seguramente se rompería en el caso de otras funciones de activación, por ejemplo, ReLu. No hay duda de que la inicialización adecuada sigue siendo un área activa de investigación.
Normalización por lotes
Esta es una idea algo relacionada con lo que hemos discutido hasta ahora. Recuerde, normalizamos la entrada antes de enviarla a nuestra red. Una de las razones por las que se hizo esto fue para tener en cuenta la inestabilidad causada en la red por el cambio de covarianza.
Explica por qué incluso después de aprender el mapeo de alguna entrada a la salida, necesitamos volver a entrenar el algoritmo de aprendizaje para aprender el mapeo de esa misma entrada a la salida en caso de que cambie la distribución de datos de la entrada.
Sin embargo, el problema no se resuelve allí sólo, ya que la distribución de datos también podría variar en capas más profundas. La activación en cada capa podría dar como resultado una distribución de datos diferente.
Por lo tanto, para aumentar la estabilidad de las redes neuronales profundas, necesitamos normalizar los datos suministrados en cada capa restando la media y dividiéndolos por la desviación estándar.
Regularización
Uno de los problemas más comunes en el entrenamiento de redes neuronales profundas es el sobreajuste. Te darás cuenta de que hay un ajuste excesivo cuando tu red funcionó excepcionalmente bien en los datos de entrenamiento pero mal en los datos de prueba.
Esto sucede cuando nuestro algoritmo de aprendizaje intenta ajustar cada punto de datos en la entrada, incluso si representan algún ruido muestreado aleatoriamente, como se muestra en la figura siguiente.

La regularización ayuda a evitar el sobreajuste al penalizar los pesos de la red. Para explicarlo más, considere una función de pérdida definida para la tarea de clasificación a través de una red neuronal como se muestra a continuación:
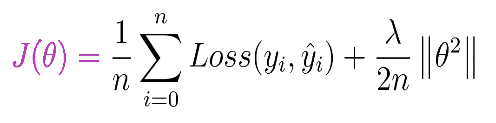
- J(theta) – Función objetivo general a minimizar.
- n: número de muestras de entrenamiento.
- y(i): etiqueta real para la i-ésima muestra de entrenamiento.
- y_hat(i): etiqueta prevista para la i-ésima muestra de entrenamiento.
- Pérdida: pérdida de entropía cruzada.
- Theta: pesos de la red neuronal.
- Lambda: parámetro de regularización.
Observe cómo se utiliza el parámetro de regularización (lambda) para controlar el efecto de los pesos en la función objetivo final. Entonces, en caso de que lambda tome un valor muy grande, los pesos de la red deben ser cercanos a cero para minimizar la función objetivo.
Pero si dejamos que los pesos colapsen a cero, anularíamos el efecto de muchas unidades en la capa y, por lo tanto, la red no es mejor que un único clasificador lineal con pocas unidades de regresión logística.
E inesperadamente, esto nos arrojará al régimen conocido como desajuste, que no es mucho mejor que el sobreajuste. Claramente, tenemos que elegir el valor de lambda con mucho cuidado para que al final nuestro modelo caiga en la categoría equilibrada (tercer gráfico de la figura).
Regularización de la deserción
Además de lo que comentamos, existe una técnica más poderosa para reducir el sobreajuste en redes neuronales profundas conocida como regularización de deserción.
La idea clave es eliminar unidades aleatoriamente mientras entrenamos la red para que trabajemos con una red neuronal más pequeña en cada iteración.
Descartar una unidad es lo mismo que ignorarlas durante la propagación hacia adelante o hacia atrás. En cierto sentido, esto impide que la red se adapte a algún conjunto específico de características.
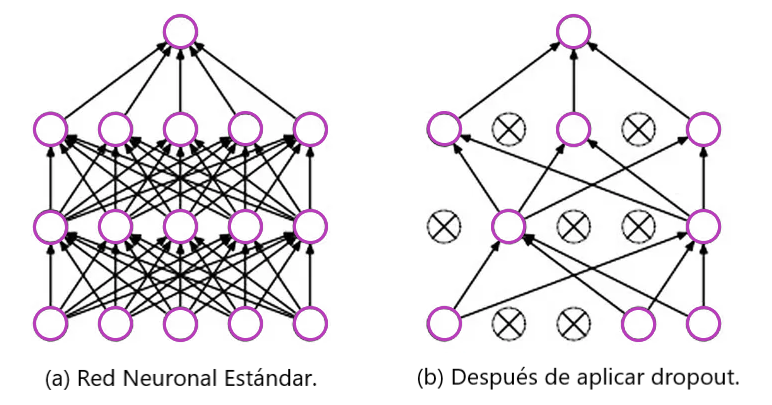
En cada iteración, eliminamos aleatoriamente algunas unidades de la red. Y en consecuencia, estamos obligando a cada unidad a no depender (no dar ponderaciones altas) en ningún conjunto específico de unidades de la capa anterior, ya que cualquiera de ellas podría activarse al azar.
Esta forma de distribuir las ponderaciones eventualmente reduce las ponderaciones a nivel de unidad individual de manera similar a lo que discutimos en la regularización L2.