¿Qué se logra en este artículo?
Lo siguiente se logra en este dataset
- Comprender la definición de Árboles de decisión
Implementación
- Cargar los datos
- Visualizar los datos usando una matriz de correlación y un par plot
- Construyendo un Decision Tree Classifier
- Determinando la precisión del modelo usando una matriz de confusión
- Visualizando el árbol de Decisión como un diagrama de flujo
¿Qué son los Árboles de Decisión?
Un árbol de decisión es una estructura tipo diagrama de flujo en la que cada nodo interno representa una “prueba” en un atributo (por ejemplo, si una moneda sale cara o cruz), cada rama representa el resultado de la prueba y cada nodo hoja representa una etiqueta de clase (decisión tomado después de calcular todos los atributos).
(Fuente: Wikipedia )
En términos más simples, un árbol de decisión verifica si un atributo o un conjunto de atributos cumple una condición y se basa en el resultado del comprobar, las verificaciones siguientes se realizan. El árbol divide los datos en diferentes partes en función de estos controles.
Árboles de Decisión: Implementación
Importación de las bibliotecas necesarias
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
import tflearn.data_utils as du
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
import seaborn as sns
from sklearn.metrics import confusion_matrix
from sklearn.externals.six import StringIO
from IPython.display import Image
from sklearn.tree import export_graphviz
import pydotplus
Lectura del dataset
data = pd.read_csv('../input/column_3C_weka.csv')
El dataset utilizado aquí es el Características biomecánicas de pacientes ortopédicos
¿Qué es la correlación?
La correlación es un término estadístico que en uso común se refiere a qué tan cerca están dos variables deben tener una relación lineal entre sí.
Por ejemplo, dos variables que son linealmente dependientes (por ejemplo, xey que dependen una de la otra como x = 2y) tendrán una correlación mayor que dos variables que no son linealmente dependiente (digamos, uyv que dependen uno del otro como u = sqr (v))
Visualizando la correlación
# Calculating the correlation matrix
corr = data.corr()
# Generating a heatmap
sns.heatmap(corr,xticklabels=corr.columns, yticklabels=corr.columns)

sns.pairplot(data)


En los dos gráficos anteriores puede ver claramente que los pares de variables independientes con una correlación más alta tienen un gráfico de dispersión más lineal que las variables independientes que tienen una correlación relativamente menor
División del dataset en independiente (x) y dependiente (y) variables
x = data.iloc[:,:6].values
y = data.iloc[:,6].values
Dividir el dataset en datos de tren y prueba
Los datos de tren para entrenar el modelo y los datos de prueba para validar el rendimiento del modelo
x_train , x_test, y_train, y_test = train_test_split(x, y, test_size = 0.25, random_state = 0)
Escalando las variables independientes
Esta pregunta sobre stackoverflow tiene respuestas que dan una breve explicación de por qué es necesario escalar y cómo puede afectar el modelo
sc = StandardScaler()
x_train = sc.fit_transform(x_train)
x_test = sc.transform(x_test)
Construyendo árboles de decisión
El criterio aquí es la entropía. El parámetro de criterio determina la función para medir la calidad de una división. Cuando se usa la entropía como criterio, cada división intenta reducir la aleatoriedad en esa parte de los datos.
Hay muchos parámetros en la clase de árbol de decisión que puede ajustar para mejorar sus resultados. Ahí tomamos un pico en el parámetro max_depth.
El max_dept determina la profundidad a la que puede llegar un árbol. El efecto de este parámetro en el modelo se analizará más adelante en este artículo
classifier = DecisionTreeClassifier(criterion = 'entropy', max_depth = 4)
classifier.fit(x_train, y_train)
Hacer la predicción en los datos de prueba
y_pred = classifier.predict(x_test)
¿Qué es una matriz de confusión?
Una matriz de confusión es una técnica para resumir el rendimiento de un algoritmo de clasificación. La precisión de la clasificación por sí sola puede ser engañosa si tiene una cantidad desigual de observaciones en cada clase o si tiene más de dos clases en su dataset. Calcular una matriz de confusión puede darle una mejor idea de cuál es su modelo de clasificación y qué tipos de errores está cometiendo.
cm = confusion_matrix(y_test, y_pred)
accuracy = sum(cm[i][i] for i in range(3)) / y_test.shape[0]
print("accuracy = " + str(accuracy))Visualizando Árboles de Decisión
dot_data = StringIO()
export_graphviz(classifier, out_file=dot_data,
filled=True, rounded=True,
special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())


Árboles de Decisión: Construcción de un modelo sin el parámetro max_depth
classifier2 = DecisionTreeClassifier(criterion = 'entropy')
classifier2.fit(x_train, y_train)
y_pred2 = classifier2.predict(x_test)
cm2 = confusion_matrix(y_test, y_pred2)
accuracy2 = sum(cm2[i][i] for i in range(3)) / y_test.shape[0]
print("accuracy = " + str(accuracy2))
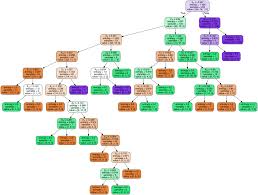
Visualizando Árboles de Decisión sin el parámetro max_depth
dot_data = StringIO()
export_graphviz(classifier2, out_file=dot_data,
filled=True, rounded=True,
special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())


Ahora, considere los nodos hoja (nodos terminales) del árbol con y sin el parámetro max_depth. Notará que la entropía de todos los nodos terminales es cero en el árbol sin el parámetro max_depth y no es cero en tres con ese parámetro.
Esto se debe a que cuando el parámetro no se menciona, la división tiene lugar recursivamente hasta que el nodo terminal tenga una entropía de cero.
Para saber más sobre los diferentes parámetros del sklearn.tree.DecisionTreeClassifier, haga clic en aquí
Para obtener este artículo como un cuaderno iPython, haga clic aquí