Algoritmo t-SNE: Introducción
Siempre he tenido una pasión por aprender y me considero un aprendiz de por vida.
Estar en SAS, como científico de datos, me permite aprender y probar nuevos algoritmos y funcionalidades que regularmente lanzamos a nuestros clientes. A menudo, los algoritmos no son técnicamente nuevos, pero son nuevos para mí, lo que hace que sea muy divertido.
Recientemente, tuve la oportunidad de aprender más sobre la incrustación de vecinos estocásticos distribuidos (t-SNE). En esta publicación voy a dar una descripción general de alto nivel del algoritmo t-SNE.
Compartiré un ejemplo de código python en el que usaré un algormitmo t-SNE en el conjunto de datos Digits y MNIST.
¿Qué es algoritmo t-SNE?
La incrustación de vecinos estocástica distribuida (t-SNE) es una técnica no lineal no supervisada utilizada principalmente para la exploración de datos y la visualización de datos de alta dimensión.
En términos más simples, t-SNE le da una sensación o intuición de cómo se organizan los datos en un espacio de alta dimensión. Fue desarrollado por Laurens van der Maatens y Geoffrey Hinton en 2008.
Algoritmo t-SNE vs PCA
Si está familiarizado con Análisis de componentes principales (PCA), entonces como yo, usted ‘ probablemente se esté preguntando la diferencia entre PCA y t-SNE.
- Lo primero a tener en cuenta es que PCA se desarrolló en 1933, mientras que t-SNE se desarrolló en 2008. Mucho ha cambiado en el mundo de la ciencia de datos desde 1933, principalmente en el ámbito del cálculo y el tamaño de los datos.
- En segundo lugar, PCA es una técnica de reducción de dimensión lineal que busca maximizar la varianza y preserva las distancias pares grandes.
En otras palabras, las cosas que son diferentes terminan muy separadas. Esto puede conducir a una visualización deficiente, especialmente cuando se trata de estructuras distribuidoras no lineales.
Piense en una estructura múltiple como cualquier forma geométrica como: cilindro, bola, curva, etc.
t-SNE difiere de PCA al preservar solo pequeñas distancias por pares o similitudes locales, mientras que PCA se preocupa por preservar distancias pares grandes para maximizar la varianza.
Laurens ilustra bastante bien el enfoque PCA y t-SNE utilizando el conjunto de datos Swiss Roll en la Figura 1 [1]. Puede ver que debido a la no linealidad de este conjunto de datos de juguete (múltiple) y la preservación de grandes distancias, PCA conservaría incorrectamente la estructura de los datos.

Cómo funciona t-SNE
Ahora que sabemos por qué podríamos usar t-SNE sobre PCA, analicemos cómo funciona t-SNE. El algoritmo t-SNE calcula una medida de similitud entre pares de instancias en el espacio de alta dimensión y en el espacio de baja dimensión.
Luego trata de optimizar estas dos medidas de similitud usando una función de costo. Vamos a dividirlo en 3 pasos básicos.
Paso 1, mida las similitudes entre puntos en el espacio de alta dimensión. Piense en un conjunto de puntos de datos dispersos en un espacio 2D (Figura 2).
Para cada punto de datos (x i ) centraremos una distribución gaussiana sobre ese punto. Luego medimos la densidad de todos los puntos (x j ) bajo esa distribución gaussiana.
Luego renormalize para todos los puntos. Esto nos da un conjunto de probabilidades (P ij ) para todos los puntos. Esas probabilidades son proporcionales a las similitudes.
Todo lo que eso significa es que si los puntos de datos x1 y x2 tienen valores iguales bajo este círculo gaussiano, entonces sus proporciones y similitudes son iguales y, por lo tanto, tienes similitudes locales en la estructura de este espacio de alta dimensión.
La distribución gaussiana o el círculo se pueden manipular usando lo que se llama perplejidad, que influye en la varianza de la distribución (tamaño del círculo) y esencialmente en el número de vecinos más cercanos. El rango normal de perplejidad está entre 5 y 50 [2].

El paso 2 es similar al paso 1, pero en lugar de usar un La distribución gaussiana usa una distribución t de Student con un grado de libertad, que también se conoce como la distribución de Cauchy (Figura 3).
Esto nos da un segundo conjunto de probabilidades (Q ij ) en el espacio de baja dimensión. Como puede ver, la distribución t de Student tiene colas más pesadas que la distribución normal.
Las colas pesadas permiten un mejor modelado de distancias muy separadas.

- El último paso es que queremos este conjunto de probabilidades del espacio de baja dimensión (Q ij ) para reflejar los del espacio de alta dimensión (P ij ) de la mejor manera posible. Queremos que las dos estructuras de mapa sean similares. Medimos la diferencia entre las distribuciones de probabilidad de los espacios bidimensionales utilizando la divergencia de Kullback-Liebler (KL). No incluiré mucho en KL, excepto que es un enfoque asimétrico que compara de manera eficiente los valores grandes P ij y Q ij . Finalmente, utilizamos el descenso de gradiente para minimizar nuestra función de costo KL.
Caso de uso para t-SNE
Ahora que sabe cómo funciona t-SNE hablemos rápidamente sobre dónde se usa. Laurens van der Maaten muestra muchos ejemplos en su presentación de video [1].
Menciona el uso de t-SNE en áreas como investigación del clima, seguridad informática, bioinformática, investigación del cáncer, etc. t-SNE podría usarse en datos de alta dimensión y luego el resultado de esas dimensiones se convierte en insumos para algún otro modelo de clasificación .
Además, t-SNE podría usarse para investigar, aprender o evaluar la segmentación. Muchas veces seleccionamos la cantidad de segmentos antes del modelado o iteramos después de los resultados. t-SNE a menudo puede mostrar una separación clara en los datos.
Esto se puede usar antes de usar su modelo de segmentación para seleccionar un número de clúster o después para evaluar si sus segmentos realmente se mantienen. t-SNE, sin embargo, no es un enfoque de agrupamiento, ya que no conserva las entradas como PCA y los valores pueden cambiar entre ejecuciones por lo que es puramente para exploración.
Ejemplo de código
A continuación se muestra un código python (Las siguientes figuras con enlace a GitHub) donde se puede ver la comparación visual entre PCA y t-SNE en los conjuntos de datos Dígitos y MNIST.
Selecciono estos dos conjuntos de datos debido a las diferencias de dimensionalidad y, por lo tanto, a las diferencias en los resultados.
También muestro una técnica en el código donde puede ejecutar PCA antes de ejecutar t-SNE. Esto se puede hacer para reducir el cálculo y típicamente reducirías hasta ~ 30 dimensiones y luego ejecutar t-SNE.
Ejecuté esto usando python y llamando a las bibliotecas SAS. Puede parecer un poco diferente de lo que estás acostumbrado y puedes ver eso en las imágenes a continuación.
Utilicé seaborn para mis visuales, lo que pensé que era genial, pero con t-SNE puedes obtener grupos realmente compactos y necesitas hacer acercamientos. Otra herramienta de visualización, como plotly, puede ser mejor si necesitas hacer zoom in
Consulte el cuaderno completo en GitHub para que pueda ver todos los pasos intermedios y tenga el código:
Paso 1 – Cargue las bibliotecas de Python. Cree una conexión al servidor SAS (llamada ‘CAS’, que es un motor distribuido en memoria). Cargue conjuntos de acciones CAS (piense en estos como bibliotecas). Lea los datos y vea la forma.

Paso 2: hasta este punto, todavía estoy trabajando en mi máquina local. Voy a cargar esos datos en el servidor CAS que mencioné. Esto me ayuda a aprovechar el entorno distribuido y obtener eficiencia en el rendimiento.
Luego realizo un análisis de PCA tanto en dígitos como en datos MNIST.

Paso 3 – Visualice nuestros resultados de PCA para ambos dígitos y MNIST


PCA en realidad hace un trabajo decente en el conjunto de datos de Dígitos y encuentra la estructura.

Como puede ver PCA en el conjunto de datos MNIST tiene un problema de ‘hacinamiento’.
Paso 4 – Ahora probemos los mismos pasos que antes, pero usando el algoritmo t-SNE



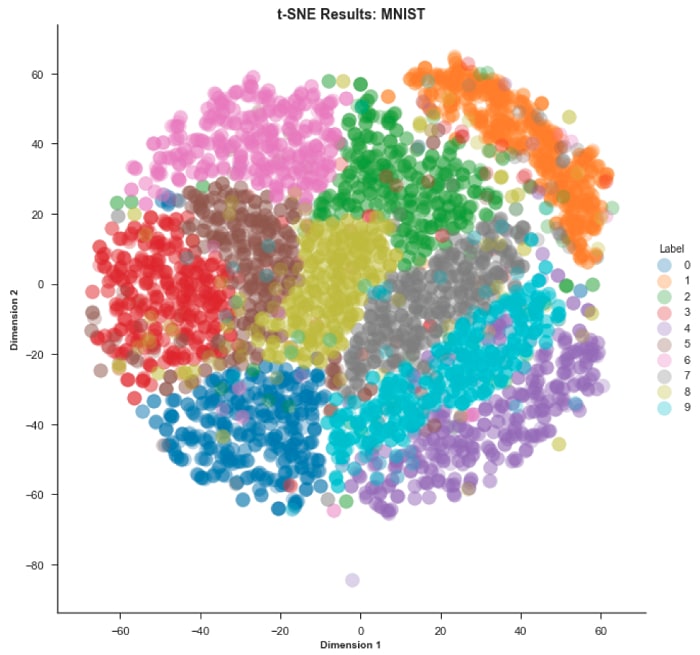
Y ahora para el conjunto de datos MNIST …


 Conclusión
Conclusión
Espero que hayan disfrutado de este resumen y ejemplo del algoritmo t-SNE. Encontré t-SNE como una herramienta de visualización muy interesante y útil, ya que casi todos los datos en los que he trabajado parecían ser de gran dimensión.