En este post veremos: ¿Qué es Regularización en Machine Learning?. Como por ejemplo Regulaciones Lasso (L1) vs Ridge (L2).
Los siguientes son los diversos pasos que caminaremos juntos y trataremos de obtener una comprensión.
- Contexto.
- Requisitos previos.
- Problema de sobreajuste.
- Objetivo.
- ¿Qué es Regularización en Machine Learning?.
- Regularización en Machine Learning de la norma L2 o Ridge.
- Norma L1 o Regularización en Machine Learning de Lasso.
- Regulaciones Lasso (L1) vs Ridge (L2).
- Conclusión.
1. Contexto
En esta publicación, consideraremos la regresión lineal como el algoritmo donde la variable objetivo ‘y’ se explicará mediante 2 características ‘x1’ y ‘x2’ cuyos coeficientes son β1 y β2.
2. Requisitos previos
En primer lugar, eliminemos algunos requisitos previos menores para comprender su uso en el futuro.
Regresión lineal
Opcional: Consulte el Capítulo 3 en el siguiente enlace para obtener más información sobre Regresión lineal.
Regresión de la función de coste de los mínimos cuadrados ordinarios (OLS)
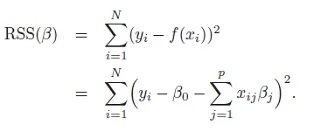
- N – número de muestras.
- p – número de variables o características independientes.
- x – característica.
- y – objetivo real o variable dependiente.
- f(x) – objetivo estimado.
- β – coeficiente o peso correspondiente a cada característica o variable independiente.
Descenso de gradiente representado como gráfico de contorno
En la figura 1 (a) a continuación, el descenso del gradiente se representa en 3 niveles. J (β) representa el error para β1 y β2 correspondientes. El color rojo representa las zonas donde el error es alto y el color azul representa las zonas donde el error es mínimo.
Usando gradiente de descenso, los coeficientes β1 y β2 se identificarían donde el error es mínimo.


En la figura 1 (b) anterior, el error correspondiente de la función de costo del descenso de gradiente se proyecta en 2-dim con los colores correspondientes.
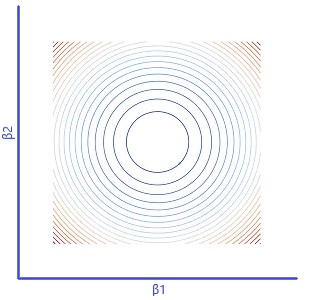
En la figura 2 de la izquierda, el contorno de descenso del gradiente para la regresión lineal simple se representa en formato bidimensional en el sistema de coordenadas de los coeficientes β1 y β2.
Dejemos de lado este entendimiento por un tiempo y pasemos a abordar algunos otros conceptos básicos.
3. Problema de sobreajuste
Suponiendo que hemos entrenado un modelo utilizando regresión lineal en el conjunto de entrenamiento y hemos aumentado el rendimiento a niveles satisfactorios, nuestro siguiente paso es validarlo con el conjunto de prueba/datos no vistos
. En la mayoría de los casos, habrá una caída en los niveles de precisión. ¿Lo que ha sucedido?
En nuestro esfuerzo por aumentar la precisión del modelo durante el entrenamiento, nuestro modelo intentaría ajustarse y aprender tantos puntos de datos como fuera posible.
En otras palabras, a medida que aumenta la bondad de ajuste, el modelo pasa de lineal a cuadrático y luego polinómico (es decir, la complejidad del modelo está creciendo).
Esto se debe al sobreajuste. La siguiente imagen del curso de aprendizaje automático de Andrew Ng ayuda a comprender esto visualmente.

El modelo de mayor grado y los coeficientes grandes aumentan significativamente la varianza, lo que lleva al sobreajuste.
4. Objetivo
Nuestro modelo debe ser robusto para predecir bien en el mundo real, es decir, a partir de datos de muestra o de datos que no se han visto durante el entrenamiento. El sobreajuste durante el entrenamiento es lo que le impide ser robusto. Para evitar este escenario de sobreajuste y aumentar la robustez del modelo, intentamos
1. Reducir los coeficientes o pesos de las características del modelo.
2. Deshacerse de las características polinómicas de alto grado del modelo.
¿Cómo logramos esto? Entra la Regularización. Exploremoslo ahora.
5. ¿Qué es Regularización en Machine Learning?
Supongamos que hemos entrenado nuestro modelo de regresión lineal e identificado los coeficientes β1 y β2 en el mínimo global. Para poder cumplir con nuestro objetivo; Si intentamos reducir los coeficientes de las características aprendidas anteriormente, el modelo pierde precisión.
Esta pérdida de precisión debe explicarse por algo más para mantener los niveles de precisión. Esta responsabilidad será asumida por la parte de Bias de la ecuación del modelo ( Sesgo: parte de la ecuación del modelo que no depende de los datos de las características ).
La parte Bias se modificará de las siguientes maneras:
1. Es necesario reducir la varianza y aumentar el sesgo: dado que la varianza es una función de los coeficientes β1, β2; El sesgo también se les asignará y cambiará en función de los coeficientes β1, β2. La razón por la que se utilizan las normas L1 y L2 de los coeficientes β1, β2.
2. Generalización: esta función de los coeficientes β1, β2 debe generalizarse y funcionar en todo el espacio de coordenadas (valores positivos y negativos en los ejes). Esa es la razón por la que encontramos el operador de módulo en las ecuaciones normales L1 y L2.
3. Parámetro de regularización ‘λ’: Dado que tanto la varianza como el sesgo son funciones de los coeficientes β1, β2, serán directamente proporcionales. Esto no funcionará. Por lo tanto, necesitamos un parámetro adicional que pueda regular el tamaño del término Bias. Este regulador es el parámetro de Regularización ‘λ’.
4. ‘λ’ es un hiperparámetro: si ‘λ’ fuera un parámetro, Gradient Descent lo establecería en 0 y viajaría al mínimo global. Por lo tanto, el control de ‘λ’ no se puede otorgar a Gradient Descent y debe mantenerse fuera. No será un parámetro sino un hiperparámetro.
Después de comprender los cambios en el término Bias, pasemos a algunas funciones de los coeficientes β1, β2 que se usarán para la regularización.
6.Norma L2 o regresión de cresta
La norma L2 es la norma de distancia euclidiana de la forma |β1|² + |β2|².
La función de Costo Modificado con Regularización en Machine Learning L2 es la siguiente:
 Fuente: https: //web.stanford.edu/~hastie/ElemStatLearn/
Fuente: https: //web.stanford.edu/~hastie/ElemStatLearn/
Supongamos que λ = 1 y está fuera de escena por un tiempo.
β1 y β2 pueden variar en el proceso de encontrar el error mínimo global. Con el término de regularización (resaltado en azul en la ecuación anterior); un valor particular de (β1,β2) generará una salida sesgada β1² + β2².
Puede haber varios valores que pueden generar el mismo sesgo como (1,0), (-1,0), (0,-1), (0,7,0,7) y (0,1). En el caso de la norma L2, las diversas combinaciones de β1 y β2 que generan un mismo sesgo particular forman un círculo. Para nuestro ejemplo, consideremos un término de sesgo = 1. La figura 6(a) representa este círculo.


La figura 6 (b) indica el gráfico de contorno de descenso de gradiente del problema de regresión lineal. Ahora bien, hay dos fuerzas actuando aquí.
- Fuerza 1: Término de sesgo que empuja a β1 y β2 para que queden en algún lugar del círculo negro únicamente.
- Fuerza 2: Descenso de gradiente intentando viajar hasta el mínimo global indicado por el punto verde.
Ambas fuerzas tiran y finalmente se asientan cerca del punto de intersección indicado por la ‘Cruz Roja’.
Recuerde que nuestros supuestos para la figura 6(b) hasta ahora eran Término de sesgo = 1 y λ = 1. Ahora elimine un supuesto relacionado con el término de sesgo.
Imagine que el ‘círculo negro’ cambia de tamaño y el descenso del gradiente se establece en un punto diferente donde el costo es mínimo. El supuesto de λ = 1 sigue vigente. Este costo mínimo observado es para λ = 1
Luego elimine el otro supuesto λ = 1. Proporcione un valor diferente, digamos λ = 0,5.
Repita el proceso de descenso de gradiente para λ = 0,5 y verifique el costo. Este proceso se puede repetir para varios valores de λ con el fin de identificar el valor óptimo de λ cuya función de costo dé el menor error.
El objetivo general es siempre tener un bajo costo después del descenso de gradiente. De ahí que se identifiquen los valores de λ, β1,β2 manteniéndolo como objetivo.
Al final de este proceso, la varianza se habrá reducido, es decir, los coeficientes se reducirán en magnitud. Pasemos a otro tipo de función de β1,β2.
7. Norma L1 o regresión de lazo
La norma L1 tiene la forma |β1| + |β2|.
La función de Costo Modificado para la Regularización en Machine Learning L1 es la siguiente:

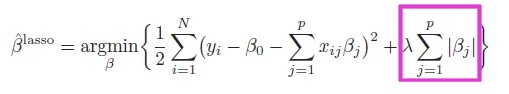
Fuente: https://web.stanford.edu/~hastie/ElemStatLearn/
La figura 7 (a) indica la forma de la Norma L1.

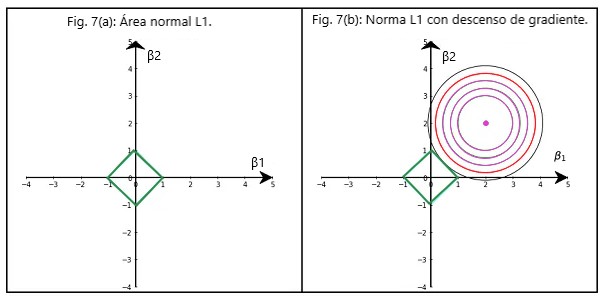
La figura 7 (b) indica la norma L1 con el gráfico de contorno de descenso de gradiente. Desde el punto de vista de la reducción de la varianza, la misma lógica analizada en la sección anterior también es válida aquí.
Pasemos a otro aspecto importante de la regularización de Lasso que analizaremos en la siguiente sección.
8. Regularización en Machine Learning de Lasso (L1) vs Ridge (L2)
La Fig. 8 (a) muestra el área de las Normas L1 y L2 juntas. Para la misma cantidad de término de Sesgo generado, el área ocupada por la Norma L1 es pequeña. Pero L1 Norm no otorga ningún espacio cerca de los ejes.
Esto es lo que hace que el punto de intersección entre la Norma L1 y el Contorno de Descenso de Gradiente converja cerca de los ejes que llevan a la selección de características.


La figura 8 (b) indica las normas L1 y L2 junto con los contornos de descenso de gradiente de diferentes problemas de regresión lineal. Excepto en un caso, la norma L1 converge en los ejes o muy cerca de ellos y, por lo tanto, elimina la característica del modelo.
Cada cuadrante aquí tiene un contorno de descenso de gradiente para un problema de regresión lineal diferente. Los colores verde, azul y marrón indican que están relacionados con diferentes problemas de regresión lineal.
El círculo ROJO en cada contorno cruza la cresta o norma L2. El círculo NEGRO en cada contorno cruza la Norma Lasso o L1.
Esto indica que la norma L1 o la regularización de lazo actúan como selector de funciones además de reducir la variación.
9. Conclusión


La reducción de la varianza es sinónimo de compensación de la varianza del sesgo.