La gran mayoría del aprendizaje profundo se realiza sobre datos euclidianos. Esto incluye tipos de datos en el dominio unidimensional y bidimensional. Pero no existimos en un mundo 1D o 2D. Todo lo que podemos observar existe en 3D. Y nuestros datos deben reflejar eso. Es hora de que el aprendizaje automático llegue a nuestro nivel.
Imágenes, texto, audio y muchos otros son todos datos euclidianos.

Los datos no euclidianos pueden representar elementos y conceptos más complejos con más precisión que la representación 1D o 2D:

Cuando representamos las cosas de una manera no euclidiana, le estamos dando un sesgo inductivo. Esto se basa en la intuición de que, dados los datos de un tipo, formato y tamaño arbitrarios. Se puede priorizar el modelo para aprender ciertos patrones cambiando la estructura de esos datos. En la mayoría de las investigaciones y publicaciones actuales, el sesgo inductivo que se utiliza es relacional.
Sobre la base de esta intuición, Geometric Deep Learning (GDL) es el campo de nicho en el marco del aprendizaje profundo que tiene como objetivo construir redes neuronales que puedan aprender de datos no euclidianos.
El ejemplo principal de un tipo de datos no euclidiano es un gráfico. Los gráficos son un tipo de estructura de datos que consta de nodos (entidades) que están conectados con bordes (relaciones). Esta estructura de datos abstracta se puede utilizar para modelar casi cualquier cosa.
Queremos poder aprender de los gráficos porque:
Los gráficos nos permiten representar características individuales. Al tiempo que brindamos información sobre las relaciones y la estructura.
Hay varios tipos de gráficos, cada uno con un conjunto de reglas, propiedades y posibles acciones. La teoría de los gráficos es el estudio de los gráficos y lo que podemos aprender de ellos. Esto será cubierto en la siguiente parte de esta serie.
Ejemplos de Geometric Deep Learning
Estas son las dos aplicaciones más populares y los enfoques de investigación en la literatura. A menudo se utilizan como puntos de referencia (no oficiales).
Modelización molecular y aprendizaje.
Para un ejemplo concreto de cómo Graph Learning puede mejorar las tareas de aprendizaje automático existentes , podemos observar las ciencias computacionales.
Uno de los cuellos de botella en la química computacional, la biología y la física son los conceptos de representación, las entidades y las interacciones. La naturaleza de la ciencia es empírica y, por lo tanto, es el resultado de muchos factores externos y relaciones. Aquí hay algunos ejemplos de dónde esto es más obvio:
- Redes de interacción de proteínas.
- Redes neuronales
- Moléculas
- Diagramas de feynman
- Mapas cosmologicos
Nuestros métodos actuales para representar estos conceptos computacionalmente pueden considerarse “con pérdidas”, ya que perdemos mucha información valiosa. Por ejemplo, usar una cadena de sistema de entrada de línea de entrada molecular (SMILE) simplificada para representar moléculas es fácil de calcular, pero a expensas de la información estructural de la molécula.
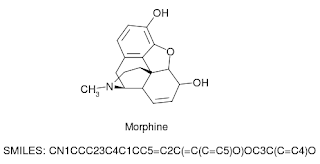
Al tratar los átomos como nodos y los enlaces como bordes. Podemos guardar información estructural que se puede usar en la predicción o clasificación.
Entonces, en lugar de usar una cadena que representa una molécula como entrada a una Red Neural Recurrente (RNN), podemos usar el gráfico molecular como entrada a su equivalente geométrico.
Modelado y aprendizaje 3D
Como ejemplo de cómo Geometric Deep Learning nos permite aprender de tipos de datos que nunca se usaron antes. Considere a una persona posando para una cámara:

Esta imagen es 2D, aunque en nuestra mente, somos conscientes de que representa a una persona en 3D. Nuestros algoritmos actuales, es decir, las redes neuronales convolucionales (CNN). Son muy buenos para predecir etiquetas como la persona que posa y / o los tipos de poses que solo tienen una imagen 2D. La dificultad surge cuando las poses se vuelven extremas y el ángulo ya no es fijo. Muchas veces puede haber ropa u objetos en una imagen que obstruyen la vista de un algoritmo, lo que dificulta la predicción de la postura.
Ahora imagine un modelo 3D de esta misma persona haciendo poses:
La CNN ahora se puede ejecutar en el objeto 3D en lugar de una imagen 2D del objeto.
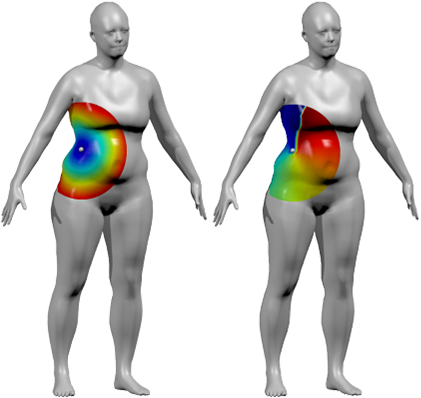
En lugar de aprender de una representación 2D, que restringe los datos a un único ángulo de perspectiva. Imagine que podríamos ejecutar una convolución directamente sobre el objeto en sí. De manera análoga a las CNN tradicionales, el núcleo pasaría a través de cada “píxel” representado como un nodo en una nube de puntos (básicamente un gráfico que envuelve el objeto 3D). Se cubrirían todos los rincones y grietas del modelo 3D y se considerará la información. En resumen, la diferencia entre las CNN de vainilla y su equivalente geométrico es predecir la etiqueta de un objeto dado una imagen de él. En lugar de predecir la etiqueta de un objeto dado un modelo 3D del mismo.
A medida que nuestra tecnología de modelado, diseño e impresión en 3D mejora. Uno podría imaginar cómo esto daría resultados mucho más precisos y precisos.
El caso de la dimensionalidad.
Dimensiones en el sentido tradicional.
La noción de dimensionalidad ya se usa comúnmente en la ciencia de datos y el aprendizaje automático. Donde el número de “dimensiones” se correlaciona con el número de características / atributos por ejemplo / punto de datos en un conjunto de datos.
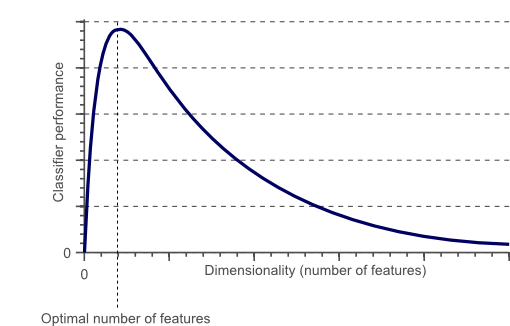
Mientras que al principio, el rendimiento de los algoritmos de aprendizaje automático aumenta, después de un cierto número de características (dimensiones), el rendimiento disminuye. Esto se conoce como la maldición de la dimensionalidad.
Geometric Deep Learning no resuelve este problema. Más bien, los algoritmos como las convoluciones de gráficos reducen las penalizaciones de rendimiento en el uso de tipos de datos que tienen muchas características, ya que los datos relacionales se consideran a través de sesgos inductivos y no como una característica adicional.
De qué hablamos cuando hablamos de dimensionalidad.
Dimensionalidad en Geometría El aprendizaje profundo es solo una cuestión de datos que se utilizan para entrenar una red neuronal. Los datos euclidianos obedecen las reglas de la geometría euclidiana, mientras que los datos no euclidianos son leales a la geometría no euclidiana.
Como se explica en esta increíble publicación de StreamExchange AI , la geometría no euclidiana se puede resumir con la frase:
“El camino más corto entre 2 puntos no es necesariamente una línea recta”.
Otras reglas extrañas incluyen:
- Los ángulos interiores de los triángulos siempre suman más de 180 grados
- Las líneas paralelas se pueden encontrar, ya sea infinitamente o nunca
- Las formas cuadriláteras pueden tener líneas curvas como lados.
Hay un campo completo de geometría no euclidiana que es otro tema en sí mismo. Para un poco de impulso de la intuición, tome una imagen, uno de los tipos de datos euclidianos más populares.

Una imagen compuesta de píxeles tiene una noción de izquierda, derecha, arriba y abajo. Uno puede atravesar la imagen traduciendo una función sobre la imagen recursivamente. Esto es exactamente lo que hace una CNN.
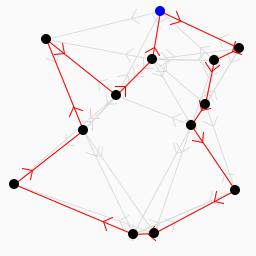
En una gráfica, sin embargo, no hay noción de izquierda, derecha, arriba o abajo. Solo hay un nodo que está conectado a un número arbitrario de nodos. Un nodo puede incluso conectarse a sí mismo.
Las dimensiones en el sentido tradicional de la máquina y el aprendizaje profundo todavía existen en el uso de datos no euclidianos para el entrenamiento de redes neuronales. Es completamente posible tener muchas características de nodo, por ejemplo, donde cada característica es otra “dimensión”. Pero el término rara vez se usa en la literatura para representar esto.
El estándar frente al nuevo
El aprendizaje automático se ha centrado en el aprendizaje profundo. Que a su vez giraba en torno a un puñado de algoritmos populares. Cada algoritmo se especializa aproximadamente en un tipo de datos específico. Al igual que las RNN se crearon para datos dependientes del tiempo y las CNN para los datos de tipo de imagen, las redes neuronales de gráficos (GNN) son un tipo de algoritmo de Geometric Deep Learning creado para gráficos y redes. Como dijo Graham Ganssle, jefe de Data Science en Expero:
Las redes convolucionales gráficas son lo mejor desde que se cortó el pan porque permiten que los algos analicen la información en su forma nativa en lugar de requerir una representación arbitraria de esa misma información en el espacio dimensional inferior que destruye la relación entre las muestras de datos, negando así sus conclusiones. - Graham Ganssle (en un Tweet)
Las redes de convolución de Graph, o GCNs, son para las redes neuronales de Graph, lo que las CNN son para las redes neuronales de Vanilla.
La implicación de este nuevo método hace una gran diferencia; Ya no estamos obligados a dejar información importante en un conjunto de datos. Información como la estructura, las relaciones y las conexiones, que son parte integral de algunas de las tareas e industrias más importantes que brindan datos, como el transporte, los medios sociales y las redes de proteínas.
En resumen, el campo Geometric Deep Learning tiene 3 contribuciones principales, podemos:
- Hacer uso de datos no euclidianos.
- Maximizar la información de los datos que recopilamos.
- Usar estos datos para enseñar algoritmos de aprendizaje automático.
En un artículo en el que se demostró que los algoritmos de aprendizaje de gráficos se pueden generalizar y modular para varias aplicaciones y aumentos, se dijo que:
Abogamos por hacer de la generalización una de las principales prioridades para la IA. Y abogamos por adoptar enfoques integradores que se basen en ideas de la cognición humana, la informática tradicional, la práctica estándar de ingeniería y el aprendizaje profundo moderno. – DeepMind, Google Brain, MIT y la Universidad de Edimburgo
En otras palabras, tenemos mucho que esperar de Geometric Deep Learning.
En esencia
Entonces, ¿qué es Geometric Deep Learning?
Geometric Deep Learning es un nicho en el Aprendizaje Profundo que apunta a generalizar los modelos de redes neuronales a dominios no euclidianos, como gráficos y múltiples.
La noción de relaciones, conexiones y propiedades compartidas es un concepto que ocurre naturalmente en los seres humanos y en la naturaleza. Entender y aprender de estas conexiones es algo que damos por sentado. Geometric Deep Learning es importante porque nos permite aprovechar los datos con relaciones, conexiones y propiedades compartidas inherentes.
Geometric Deep Learning: Puntos clave
- El dominio euclidiano y el dominio no euclidiano tienen diferentes reglas que se siguen; los datos en cada dominio se especializan en ciertos formatos (imagen, texto frente a gráficos, variedades) y transmiten diferentes cantidades de información
- Geometric Deep Learning es la clase de Aprendizaje profundo que puede operar en el dominio no euclidiano con el objetivo de enseñar a los modelos cómo realizar predicciones y clasificaciones en tipos de datos relacionales
- La diferencia entre el Aprendizaje profundo tradicional y Geometric Deep Learning se puede ilustrar imaginando la precisión entre escanear una imagen de una persona en lugar de escanear la superficie de la misma persona.
- En el Aprendizaje profundo tradicional, la dimensionalidad está directamente relacionada con el número de características en los datos. Mientras que en Geometric Deep Learning, se refiere al tipo de datos en sí, no al número de características que tiene.
Una de las razones por las que me propuse escribir sobre Geometric Deep Learning es que casi no hay recursos, tutoriales o guías de nivel de entrada para este nicho relativamente nuevo. Con ese objetivo final en mente, estoy escribiendo una serie de artículos en Graph Learning.
Aprendizaje profundo 🤖 en gráficos y en 3D
Continúa leyendo en Hacia la ciencia de datos »
