Introducción

En este Proyecto Machine Learning, desarrollaremos y evaluaremos el rendimiento y el poder predictivo de un modelo entrenado y probado sobre los datos recopilados de las casas en los suburbios de Boston.

Una vez que obtengamos un buen ajuste, usaremos este modelo para predecir sobre el valor monetario de una casa que se encuentra en esa ubicación.

Un modelo como este sería muy valioso para un agente de bienes raíces que podría hacer uso de la información proporcionada diariamente.

Usted puede encontrar el proyecto completo, la documentación y el conjunto de datos en mi página de GitHub .

Obtención de los datos y el preprocesamiento anterior

El conjunto de datos de este modelo proviene del Repositorio de aprendizaje de máquinas de la UCI. Estos datos se recopilaron en 1978 y cada una de las 506 entradas representa datos agregados sobre 14 características para hogares de diversos suburbios en Boston.

Esta es una descripción general del conjunto de datos original, con sus características originales:

Con el propósito de este Proyecto Machine Learning se realizaron los siguientes pasos de preprocesamiento:

Las características esenciales para el Proyecto Machine Learning son: ‘RM’, ‘LSTAT’, ‘PTRATIO’ y ‘MEDV’. Se han excluido las características restantes.
Se han eliminado 16 puntos de datos con un valor ‘MEDV’ de 50.0. Como es probable que contengan valores censurados o faltantes.
1 punto de datos con un valor de ‘RM’ de 8.78 se considera un valor atípico y se eliminó para el rendimiento óptimo del modelo.
Dado que se trata de datos obsoletos , el valor ‘MEDV’ se ha escalado multiplicativamente para dar cuenta de los 35 años de inflación de markt.

Ahora abriremos un cuaderno Jupyter de python 3 y ejecutaremos el siguiente fragmento de código para cargar el conjunto de datos y eliminar las características no esenciales. . Recibiendo un mensaje de éxito si las acciones se realizaron correctamente.

Como nuestro objetivo es desarrollar un modelo que tenga la capacidad de predecir el valor de las casas, dividiremos el conjunto de datos en características y la variable objetivo. Y almacénelos en características y precios, respectivamente

Las características ‘RM’, ‘LSTAT’ y ‘PTRATIO’ nos dan información cuantitativa sobre cada punto de datos. Los almacenaremos en características .
La variable objetivo, “MEDV”, será la variable que buscamos predecir. Lo almacenaremos en precios .

# Import libraries necessary for this project import numpy as np import pandas as pd from sklearn.model_selection import ShuffleSplit

# Import supplementary visualizations code visuals.py import visuals as vs

# Pretty display for notebooks %matplotlib inline

# Load the Boston housing dataset data = pd.read_csv('housing.csv') prices = data['MEDV'] features = data.drop('MEDV', axis = 1)

# Success print("Boston housing dataset has {} data points with {} variables each.".format(*data.shape))

Exploración de datos

En la primera sección del Proyecto Machine Learning, haga un análisis exploratorio del conjunto de datos y proporcione algunas observaciones.

Calcule estadísticas
# Minimum price of the data minimum_price = np.amin(prices)

# Maximum price of the data maximum_price = np.amax(prices)

# Mean price of the data mean_price = np.mean(prices)

# Median price of the data median_price = np.median(prices)

# Standard deviation of prices of the data std_price = np.std(prices)

# Show the calculated statistics print("Statistics for Boston housing dataset:\n") print("Minimum price: ${}".format(minimum_price)) print("Maximum price: ${}".format(maximum_price)) print("Mean price: ${}".format(mean_price)) print("Median price ${}".format(median_price)) print("Standard deviation of prices: ${}".format(std_price))

Feature Observation

Cada punto de datos representa a El vecindario de Boston diferente y cada una de las tres características utilizadas representan:

‘RM’ es la número total de habitaciones entre hogares en el vecindario.
‘LSTAT’ es el porcentaje de propietarios en el vecindario considerado de clase baja.
‘PTRATIO’ es la proporción de estudiantes a maestros en primaria y escuelas secundarias en la vecindad.

La ciencia de datos es el proceso de hacer varias suposiciones e hipótesis sobre los datos y probarlos realizando algunas tareas. Inicialmente, podríamos hacer las siguientes suposiciones intuitivas para cada función:

Las casas con más habitaciones (valor más alto de ‘RM’) valdrán más. Por lo general, las casas con más habitaciones son más grandes y pueden acomodar a más personas, por lo que es razonable que cuesten más dinero. Son variables directamente proporcionales.
Las vecindades con más trabajadores de clase baja (mayor valor de ‘LSTAT’) valdrán menos. Si el porcentaje de personas de la clase trabajadora más baja es más alto, es probable que tengan un poder adquisitivo bajo y, por lo tanto, las casas cuesten menos. Son variables inversamente proporcionales.
Los vecindarios con más proporción de estudiantes por maestro (mayor valor de ‘PTRATIO’) valdrán menos. Si el porcentaje de estudiantes por maestro es mayor, es probable que en el vecindario haya menos escuelas, esto podría deberse a que hay menos impuestos, pero esto podría deberse a que en ese vecindario las personas ganan menos dinero. Si las personas ganan menos dinero, es probable que sus casas valgan menos. Son variables inversamente proporcionales.

Descubriremos si estas suposiciones son precisas a través del Proyecto Machine Learning.

Análisis exploratorio de datos

Diagrama de dispersión e histogramas

Comenzaremos creando una matriz de diagrama de dispersión que nos permitirá visualizar las relaciones y correlaciones por pares entre las diferentes características.

También es bastante útil tener una visión general rápida de cómo se distribuyen los datos y si se mantienen o no atípicos.

import matplotlib.pyplot as plt import seaborn as sns

%matplotlib inline

# Calculate and show pairplot sns.pairplot(data, size=2.5) plt.tight_layout()

Matriz de correlación

Vamos a crear ahora una matriz de correlación para cuantificar y resumir las relaciones entre las variables.

Esta matriz de correlación está estrechamente relacionada con la matriz de covarianza, de hecho, es una versión reescalada de la matriz de covarianza, calculada a partir de características estandarizadas.

Es una matriz cuadrada (con el mismo número de columnas y filas) que contiene el coeficiente de correlación r de la persona.

# Calculate and show correlation matrix cm = np.corrcoef(data.values.T) sns.set(font_scale=1.5) hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 15}, yticklabels=cols, xticklabels=cols)

Desarrollando un modelo

En esta segunda sección del Proyecto Machine Learning, desarrollaremos las herramientas y técnicas necesarias para una Modelo para hacer una predicción. Ser capaz de realizar evaluaciones precisas del desempeño de cada modelo mediante el uso de estas herramientas y técnicas ayuda a reforzar en gran medida la confianza en las predicciones.

Definición de una métrica de rendimiento

Es difícil medir la Calidad de un modelo dado sin cuantificar su desempeño en la capacitación y pruebas. Esto se hace normalmente utilizando algún tipo de métrica de rendimiento, ya sea mediante el cálculo de algún tipo de error, la bondad del ajuste o alguna otra medida útil.

Para este Proyecto Machine Learning, calcularemos el coeficiente de determinación R², para cuantificar el rendimiento del modelo. El coeficiente de determinación para un modelo es una estadística útil en el análisis de regresión, ya que a menudo describe qué tan “bueno” es el modelo para hacer predicciones.

Los valores para R² varían de 0 a 1, lo que captura el porcentaje de correlación al cuadrado entre los valores predichos y reales de la variable objetivo. Un modelo con un R² de 0 no es mejor que un modelo que siempre predice la media de la variable objetivo mientras que un modelo con un R² de 1 predice perfectamente la variable objetivo. Cualquier valor entre 0 y 1 indica qué porcentaje de la variable objetivo, usando este modelo, puede explicarse por las características.

A un modelo también se le puede dar un R2 negativo, lo que indica que el modelo es arbitrariamente peor una que siempre predice la media de la variable objetivo.

# Import 'r2_score'

from sklearn.metrics import r2_score

def performance_metric(y_true, y_predict): """ Calculates and returns the performance score between true (y_true) and predicted (y_predict) values based on the metric chosen. """

score = r2_score(y_true, y_predict)

# Return the score return score

Reproducción aleatoria y división de datos

Para esta sección, tomaremos el conjunto de datos de viviendas de Boston y dividiremos los datos en entrenamientos y pruebas de subconjuntos . Por lo general, los datos también se barajan en un orden aleatorio al crear los subconjuntos de entrenamiento y prueba para eliminar cualquier sesgo en el orden del conjunto de datos.

# Import 'train_test_split' from sklearn.model_selection import train_test_split

# Shuffle and split the data into training and testing subsets X_train, X_test, y_train, y_test = train_test_split(features, prices, test_size=0.2, random_state = 42)

print("Training and testing split was successful.")

Entrenamiento y pruebas

Puede preguntar ahora:

¿Cuál es el beneficio de dividir un conjunto de datos en una proporción de subconjuntos de capacitación y pruebas para un algoritmo de aprendizaje?

Es útil evaluar nuestro modelo una vez que está entrenado. Queremos saber si se ha aprendido correctamente de una división de entrenamiento de los datos.

Puede haber 3 situaciones diferentes:

El modelo no aprendió bien sobre los datos y no puede predecir ni siquiera los resultados del conjunto de capacitación. Esto se denomina falta de equipamiento y se debe a un alto sesgo.
El modelo aprende demasiado bien los datos de entrenamiento, hasta el punto en que los memorizó y no puede generalizar los datos nuevos. Esto se llama sobreajuste, se debe a una alta varianza.
El modelo acaba de tener el equilibrio correcto entre sesgo y varianza. Aprendió bien y puede predecir correctamente los resultados de los nuevos datos.

Análizando el desempeño del modelo

En esta tercera sección del Proyecto Machine Learning. Veremos varios modelos ‘aprendiendo y probando rendimientos en varios subconjuntos de datos de entrenamiento.

Además, investigaremos un algoritmo en particular con un aumento de & # 039; max_depth & # 039; parámetro en el conjunto completo de entrenamiento para observar cómo la complejidad del modelo afecta el rendimiento.

Graficar el rendimiento del modelo en función de diversos criterios puede ser beneficioso en el proceso de análisis. Como visualizar comportamientos que pueden no ser evidentes a partir de los resultados solo.

Curvas de aprendizaje

La siguiente celda de código produce cuatro gráficos para un modelo de árbol de decisión con diferentes profundidades máximas. Cada gráfico visualiza las curvas de aprendizaje del modelo para el entrenamiento y las pruebas a medida que aumenta el tamaño del conjunto de entrenamiento.

Tenga en cuenta que la región sombreada de una curva de aprendizaje denota la incertidumbre de esa curva (medida como la desviación estándar). El modelo se califica tanto en los conjuntos de entrenamiento como en los de prueba utilizando R2, el coeficiente de determinación.

# Produce learning curves for varying training set sizes and maximum depths vs.ModelLearning(features, prices)

Aprendiendo los datos

Si observamos de cerca la gráfica con la profundidad máxima de 3:

A medida que aumenta el número de puntos de entrenamiento, la puntuación de entrenamiento disminuye. En contraste, la puntuación de la prueba aumenta.
Como ambas puntuaciones (entrenamiento y pruebas) convergen, de los 300 puntos de dominio, tener más puntos de entrenamiento no beneficiará al modelo.
En general, con más columnas para cada uno observación. Obtendremos más información y el modelo podrá aprender mejor del conjunto de datos y, por lo tanto, hacer mejores predicciones.

Curvas de complejidad

La siguiente celda de código produce un gráfico para un modelo de árbol de decisión que ha sido entrenado y validado en los datos de entrenamiento utilizando diferentes profundidades máximas. El gráfico produce dos curvas de complejidad: una para entrenamiento y otra para validación.

Similar a las curvas de aprendizaje las regiones sombreadas de ambas curvas de complejidad denotan la incertidumbre en esas curvas y el modelo está calificado tanto en el conjunto de entrenamiento como en el de validación usando la función performance_metric.

# Produce complexity curve for varying training set sizes and maximum depths vs.ModelComplexity(X_train, y_train)

Compensación de sesgo-varianza

Si analizamos cómo la variación de sesgo varía con la profundidad máxima, podemos inferir que:

Con la profundidad máxima de uno, el gráfico muestra que el modelo no devuelve una buena puntuación en los datos de entrenamiento ni de prueba. Que es un síntoma de fallas y por lo tanto, alto sesgo. Para mejorar el rendimiento, deberíamos aumentar la complejidad del modelo. En este caso, aumentar el hiperparámetro max_depth para obtener mejores resultados.
Con la profundidad máxima de diez, el gráfico muestra que el modelo aprende perfectamente a partir de los datos de entrenamiento (con una puntuación cercana a uno) y también devuelve resultados deficientes en los datos de prueba. Que es un indicador de sobrealimentación, al no poder generalizar bien en datos nuevos. Este es un problema de alta varianza. Para mejorar el rendimiento, deberíamos disminuir la complejidad del modelo. En este caso disminuyendo el hiperparámetro max_depth para obtener mejores resultados.

Modelo óptimo de mejor conjetura

De la curva de complejidad, podemos inferir que la mejor profundidad máxima para el modelo es 4. Ya que es la que produce la mejor puntuación de validación.

Además, para una mayor profundidad, aunque la puntuación de entrenamiento aumenta. La puntuación de validación tiende a disminuir, lo que es un signo de sobreajuste.

Evaluación de desempeño del modelo

En esta sección final del Proyecto Machine Learning, construiremos un modelo y haremos una predicción sobre el conjunto de características del cliente utilizando un modelo optimizado de fit_model.

Búsqueda de cuadrícula o Grid Search

La técnica de búsqueda de cuadrícula genera candidatos de manera exhaustiva a partir de una cuadrícula de valores de parámetros especificados con el parámetro param_grid, que es un diccionario con los valores de los hiperparámetros que se deben evaluar. Un ejemplo puede ser:

param_grid = [ {‘C’: [1, 10, 100, 1000], ‘kernel’: [‘linear’]}, {‘C’: [1, 10, 100, 1000], ‘gamma’: [0.001, 0.0001], ‘kernel’: [‘rbf’]}, ]

En este ejemplo, se deben explorar dos cuadrículas: una con un kernel lineal y valores de C de [1,10,100,1000]y la segunda con un kernel RBF, y el producto cruzado de valores de C que varía en [1, 10, 100, 1000] y valores de gamma en [0.001, 0.0001].

Al ajustarlo en un conjunto de datos, se evalúan todas las combinaciones posibles de valores de parámetros y se conserva la mejor combinación.

Validación cruzada

La validación cruzada por K-fold es una técnica utilizada para Asegurándose de que nuestro modelo esté bien entrenado, sin utilizar el equipo de prueba.

Consiste en dividir los datos en k particiones de igual tamaño. Para cada partición i, entrenamos el modelo en los parámetros k-1 restantes y lo evaluamos en la partición i. El puntaje final es el promedio de los puntajes K obtenidos.

Al evaluar diferentes hiperparámetros para estimadores, todavía existe un riesgo de sobreajuste en el conjunto de prueba porque los parámetros se pueden ajustar hasta que el estimador funcione de manera óptima.

De esta manera, el conocimiento sobre el conjunto de pruebas puede “filtrarse” en el modelo y las métricas de evaluación ya no informan sobre el rendimiento de la generalización.

Para resolver este problema, otra parte del conjunto de datos puede mantenerse como una llamada “validación”. conjunto ”: la capacitación continúa con el conjunto de capacitación, después de lo cual la evaluación se realiza en el conjunto de validación, y cuando el experimento parece tener éxito, la evaluación final se puede realizar en el conjunto de prueba.

Sin embargo, al dividir los datos disponibles en tres conjuntos (entrenamiento, validación y prueba de conjuntos), reducimos drásticamente el número de muestras que se pueden usar para aprender el modelo. Y es posible que el modelo resultante no esté lo suficientemente bien entrenado (no adecuado).

Al utilizar la validación de k-fold nos aseguramos de que el modelo utilice todos los datos de entrenamiento disponibles para ajustar el modelo, puede ser computacionalmente costoso pero permite entrenar modelos incluso si hay poca información disponible.

El propósito principal de la validación de k-fold es obtener una u estimación parcial de la generalización del modelo en nuevos datos.

Ajustar un modelo

La implementación final requiere que juntemos todo y formemos un modelo utilizando el algoritmo del árbol de decisión .

Para asegurarnos de que estamos produciendo un modelo optimizado. Entrenaremos el modelo utilizando la técnica de búsqueda en cuadrícula para optimizar el parámetro & # 039; max_depth & # 039; para el árbol de decisión.

El max_depth se puede pensar en el parámetro como en cuántas preguntas se le permite al algoritmo del árbol de decisión preguntar sobre los datos antes de hacer una predicción.

Además, encontraremos que su implementación está usando ShuffleSplit () para una forma alternativa de validación cruzada ( vea la variable cv_sets). La implementación de ShuffleSplit () a continuación creará 10 (n_splits) conjuntos aleatorios, y para cada orden aleatoria, el 20% (test_size) de los datos se usará como conjunto de validación .

# Import 'make_scorer', 'DecisionTreeRegressor', and 'GridSearchCV' from sklearn.tree import DecisionTreeRegressor from sklearn.metrics import make_scorer from sklearn.model_selection import GridSearchCV

def fit_model(X, y): """ Performs grid search over the 'max_depth' parameter for a decision tree regressor trained on the input data [X, y]. """

# Create cross-validation sets from the training data cv_sets = ShuffleSplit(n_splits = 10, test_size = 0.20, random_state = 0)

# Create a decision tree regressor object regressor = DecisionTreeRegressor()

# Create a dictionary for the parameter 'max_depth' with a range from 1 to 10 params = {'max_depth':[1,2,3,4,5,6,7,8,9,10]}

# Transform 'performance_metric' into a scoring function using 'make_scorer' scoring_fnc = make_scorer(performance_metric)

# Create the grid search cv object --> GridSearchCV() grid = GridSearchCV(estimator=regressor, param_grid=params, scoring=scoring_fnc, cv=cv_sets)

# Fit the grid search object to the data to compute the optimal model grid = grid.fit(X, y)

# Return the optimal model after fitting the data return grid.best_estimator_

Haciendo predicciones

Una vez que un modelo ha sido entrenado en un conjunto dado de datos. Ahora se puede usar para hacer predicciones en nuevos conjuntos de datos de entrada.

En el caso de un regresor de árbol de decisión el modelo ha aprendido cuáles son las mejores preguntas para hacer sobre los datos de entrada y puede responder con una predicción para la variable objetivo .

Podemos usar estas predicciones para obtener información sobre los datos donde se desconoce el valor de la variable objetivo, como los datos en los que no se entrenó el modelo.

Modelo óptimo

El siguiente fragmento de código encuentra la profundidad máxima que devuelve el modelo óptimo.

# Fit the training data to the model using grid search reg = fit_model(X_train, y_train)

# Produce the value for 'max_depth' print("Parameter 'max_depth' is {} for the optimal model.".format(reg.get_params()['max_depth']))() )))

Predecir precios de venta

Imagine que éramos somos un agente de bienes raíces en el área de Boston busca usar este modelo para ayudar a ponerle un precio a las casas que son propiedad de nuestros clientes que desean vender. Hemos recopilado la siguiente información de tres de nuestros clientes:

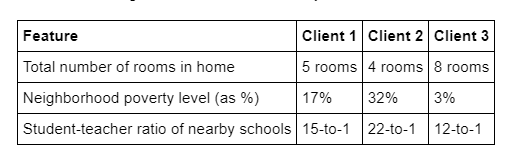
¿A qué precio recomendaríamos a cada cliente que vendiera su casa?
¿Estos precios parecen razonables dados los valores de las características respectivas?

Para averiguar las respuestas de estas preguntas ejecutaremos el siguiente fragmento de código y analizaremos su salida.

# Produce a matrix for client data client_data = [[5, 17, 15], # Client 1 [4, 32, 22], # Client 2 [8, 3, 12]] # Client 3

# Show predictions for i, price in enumerate(reg.predict(client_data)): print("Predicted selling price for Client {}'s home: ${:,.2f}".format(i+1, price))

A partir de los cálculos estadísticos realizados al inicio del Proyecto Machine Learning.

Encontramos la siguiente información :

Precios:

mínimo: $ 105000.0
máximo: $ 1024800.0
medio: $ 454342.9447852761
mediano $ 438900.0
Desviación estándar de precios: $ 165340.27765266786
En estas categorías se inscribe en este artículo. El precio de venta para el cliente 3 está cerca del millón de dólares, que está cerca del máximo del conjunto de datos. Este es un precio razonable debido a sus características (8 habitaciones, nivel de pobreza muy bajo y bajo índice de alumnos por maestro), la casa puede estar en un vecindario rico.
El precio de venta para el cliente 2 es el más bajo de los tres y se da sus características son razonables ya que se encuentran cerca del mínimo del conjunto de datos.
Para el cliente 1, podemos ver que sus características son intermedias entre las 2 últimas y, por lo tanto, su precio está bastante cerca de la media y la mediana.

Y nuestras suposiciones iniciales de las características están confirmadas:

‘RM’, tiene una relación directa proporcional con la variable dependiente ‘Precios’.
En contraste, ‘LSTAT’ y ‘PTRATIO’ tienen una relación inversamente proporcional con el variable dependiente ‘PRECIOS’.

Sensibilidad del modelo

Un modelo óptimo no es necesariamente un modelo robusto. Algunas veces, un modelo es demasiado complejo o demasiado simple como para generalizar suficientemente a nuevos datos.

Algunas veces, un modelo puede usar un algoritmo de aprendizaje que no es apropiado para la estructura de los datos dados.

Otras veces, los datos en sí mismo podría ser demasiado ruidoso o contener muy pocas muestras para permitir que un modelo capture adecuadamente la variable objetivo, es decir, el modelo está mal equipado.

La celda de código a continuación ejecuta la función fit_model diez veces con diferentes conjuntos de entrenamiento y pruebas para ver cómo la predicción para un cliente específico cambia con respecto a los datos sobre los que está capacitado.

vs.PredictTrials(features, prices, fit_model, client_data)

Obtuvimos un rango de precios de casi 70k $, I cree que esta es una desviación bastante grande ya que representa aproximadamente un 17% del valor medio de los precios de la vivienda.

Aplicabilidad del modelo

Ahora, usamos estos resultados para discutir si el modelo construido debería o shoul No se puede utilizar en un entorno del mundo real. Algunas preguntas que vale la pena responder son:

¿Qué tan relevantes son los datos recopilados a partir de 1978? ¿Qué importancia tiene la inflación?

Los datos recopilados a partir de 1978 no tienen mucho valor en el mundo actual, la sociedad y la economía han cambiado mucho y, además, la inflación ha tenido un gran impacto en los precios.

¿Son las características presentes en los datos suficientes para describir una casa? ¿Crees que factores como la calidad de las aplicaciones en el hogar, los pies cuadrados del área de la parcela, la presencia de piscinas o no, etc. deberían tener en cuenta?

El conjunto de datos considerado es bastante limitado, hay muchas características como la tamaño de la casa en pies cuadrados, la presencia de piscina o no y otros, que son muy relevantes cuando se considera el precio de una vivienda.

¿Es el modelo lo suficientemente robusto para hacer predicciones consistentes?

Dado La alta varianza en el rango de Prince puede asegurarnos de que no es un modelo sólido y, por lo tanto, no es apropiado para hacer predicciones.

¿Los datos recopilados en una ciudad urbana como Boston serían aplicables en una ciudad rural?

Los datos recopilados de una gran ciudad urbana como Boston no serían aplicables en una ciudad rural. Ya que el valor igual de los precios de las vacaciones es mucho mayor en el área urbana.

¿Es justo juzgar? El precio de una vivienda individual basado en las características de la casa. ire neighborhood?

En general, no es justo estimar o predecir el precio de una vivienda individual según las características de todo el vecindario. En el mismo vecindario puede haber grandes diferencias en los precios.

Conclusión

A lo largo de este artículo, hicimos para este Proyecto Machine Learning una regresión de aprendizaje automático de punta a punta y aprendimos y obtuvimos varias ideas sobre los modelos de regresión y cómo se desarrollan.

Este fue el primer Proyecto Machine Learning que se desarrolla en esta serie. Si te gustó, ¡estad atentos para el próximo artículo! El cual será una introducción a la teoría y los conceptos relacionados con el aprendizaje no supervisado.