En este tutorial quiero mostrarle cómo puede entrenar redes neuronales para realizar la función de puertas lógicas de una red. Voy a sumergirme en el propósito de cada neurona individual en la red y demostrar que ninguna se desperdicia.
Fundamentaremos esto utilizando un ejemplo de problema de Tensorflow Playground para que pueda implementar y experimentar con esta idea usted mismo.
Las puertas lógicas son la base de cualquier computadora moderna. El dispositivo que está usando para leer este artículo lo está usando con certeza.
Una de las mejores cosas de estas puertas es su fácil interpretación. Muchas de estas puertas se nombran en inglés simple, como las puertas AND, NOT y OR. Otros están escritos de manera menos familiar, pero aún son simples. Estas puertas lógicas se resumen en la tabla a continuación para que podamos consultarlas más adelante.
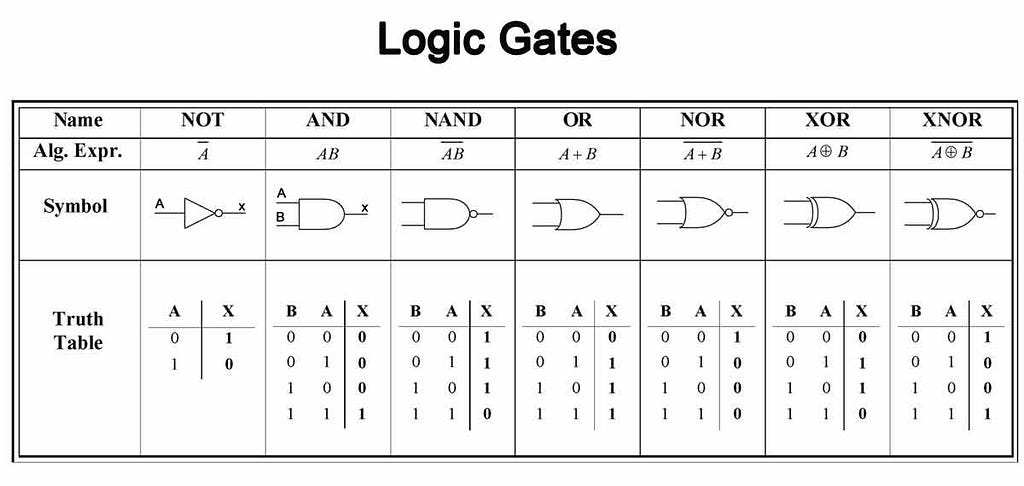
Las redes neuronales, por otro lado, se cree que son la base de cualquier cerebro moderno (o de otro tipo), y a menudo se consideran cajas negras impenetrables.
A menudo no está claro qué está haciendo una sola neurona, mientras que es obvio lo que está haciendo una única puerta lógica. Sin embargo, el funcionamiento interno de una red neuronal no necesita ser tan misterioso, y en algunos casos la estructura de la red neuronal puede ser lo suficientemente simple como para captar completamente y diseñar.
En este tutorial voy a usar una red neuronal para emular el comportamiento de una red de puertas lógicas. Vamos a ver exactamente qué hace cada neurona de la red y cómo encaja en el todo. Usando este ejemplo, espero que obtengan una mejor idea de lo que sucede dentro de las redes neuronales.
NB. Si desea ir directamente al experimento Tensorflow Playground, desplácese hasta la sección “Su turno” de este artículo.
Motivación: ¿cuándo podría funcionar una red neuronal entrenada como un sistema de puertas lógicas?
Digamos que tiene un conjunto de datos que son solo variables categóricas. Podría ser registros médicos en los que cada paciente tiene una categoría de sexo (masculino, femenino), grupo de edad (0-5, 5-10, 10-15 … 45-50 …), conteo de glóbulos blancos (alto, medio, bajo) ), etc.
Su tarea podría ser utilizar esta información para predecir qué pacientes corren el riesgo de contraer la gripe este año y, por lo tanto, deben vacunarse contra la gripe. Como es habitual con las variables categóricas, usaríamos una codificación en caliente y el registro para cada paciente es un vector de unos y ceros.
Ahora podríamos imaginar la codificación de una red lógica para estos datos a mano. Usaremos nuestras reglas comerciales para definir quién creemos que es y no está en riesgo por la gripe.
Podríamos llegar a algo como lo siguiente, donde una predicción de 1 indica que el paciente es un riesgo y una predicción 0 significa que no están en riesgo.
- Si la edad es de 25-30 Y [19659012] el recuento de glóbulos blancos es bajo LUEGO predicen 1
- Si la edad es 0-5 ENTONCES predicen 1
- Si la edad es 65 -70 Y sexo es masculino ENTONCES predicen 1
- …
- Else predicen 0
Nuestra red lógica podría verse así en Python, codificando todas las condiciones que podrían poner usted está en riesgo de contraer la gripe
at_risk = (age_is_25_30 & white_blood_cell_is_low) or (age_is_0_5) or (age_is_65_70 & sex_is_male) or ...
Podríamos programar esta red lógica si tuviéramos una gran cantidad de experiencia en el dominio, o si hicimos una gran cantidad de análisis descriptivos usando nuestros registros médicos.
Sin embargo, tratar de evitar la codificación rigurosa de esta red, que usaría grandes recursos de conocimiento de dominio experto, tiempo de desarrollador y podría introducir muchos sesgos, es la razón por la que nosotros, como modeladores, construimos modelos en primer lugar.
No queremos tener que codificar esta red lógica, pero sería bueno si alguien o alguna otra cosa pudiera hacerlo por nosotros de manera sistemática.
(Ingrese a la red neuronal, etapa derecha)
Entonces, ¿cómo funciona? una red neuronal se convierte en una red lógica?
En esta sección, voy a suponer que al menos se siente un poco cómodo con las ideas de las redes neuronales. Presentaré las palabras sesgo, peso y función de activación y no me tomaré el tiempo para explicar lo que quiero decir más allá de este simple diagrama.
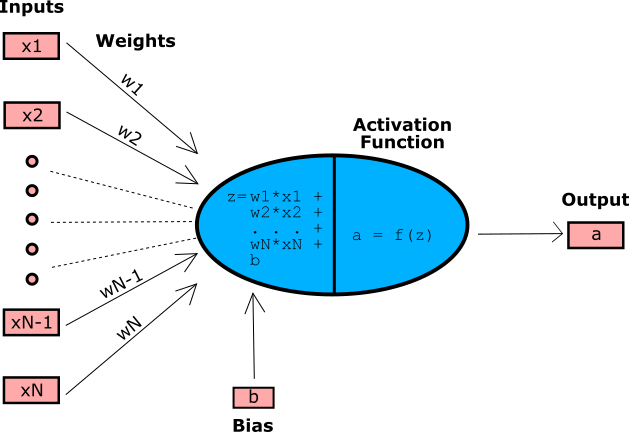
para que la red neuronal se convierta en una red lógica, tenemos que mostrar que una neurona individual puede actuar como una puerta lógica individual.
Para mostrar que una red neuronal puede llevar a cabo cualquier operación lógica sería suficiente para mostrar que una neurona puede funcionar como una puerta NAND (que puede).
Sin embargo, para hacer las cosas más bellas y comprensibles, profundicemos y demostremos cómo una neurona puede actuar como cualquiera de un conjunto de puertas que necesitaremos, a saber, las puertas AND y OR, así como una puerta de comparación de x> 0. [19659002] Vamos a fundamentar esto en un simple ejemplo concreto. Para hacer esto, me gustaría vincularlo con un conjunto de datos en particular en Tensorflow Playground .
A continuación, se muestra una imagen de un conjunto generado de datos de esta distribución. Los puntos de datos anaranjados tienen un valor de -1 y los puntos azules tienen un valor de +1. Me referiré a las coordenadas a lo largo del eje x como la variable x1, y las coordenadas a lo largo del eje y como la variable x2.
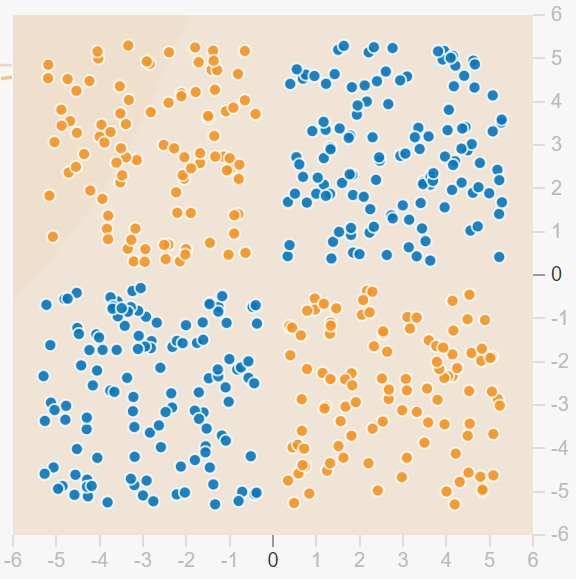
En la figura anterior puede ver que la variable objetivo es positivo cuando tanto x1 como x2 son positivos o donde tanto x2 como x1 son negativos. Si tuviéramos que codificar esto utilizando una red lógica, podríamos elegir la lógica
- If (x1> 0) Y (x2> 0) ENTONCES predecir +1
- Si (x1 <0) Y (x2 <0) ENTONCES predicen +1
- Else predicen -1
En Python podríamos escribir esta lógica como
expresión = lambda x1, x2: \ (((x1> 0) & (x2> 0)) o (! (x1> 0) &! (x2> 0))) * 2 -1
Si está familiarizado con las puertas lógicas, puede observar que una parte interna de esta expresión es una puerta XNOR.
XNOR = lambda A, B: (A y B) o (! A & B)
Qué Quiero mostrarles que podemos construir una red neuronal eficiente para esta expresión lógica.
Por supuesto, en este ejemplo, lo más obvio sería usar la función cruzada x1 * x2 y hacer predicciones con esto. Sin embargo, lo que quiero mostrar es que es posible una buena solución sin usar x1 * x2, y sumergirme en la estructura e interpretación de la red que surge cuando esta función no se crea.
También tenga en cuenta que la red neuronal lógica que vamos a crear podría ampliarse para usar 3 variables o más. Podría imaginarse que necesita la variable que es una puerta XNOR de 3 entradas que no pudimos crear cruzando características entre pares de dos variables.
Tampoco nos gustaría hacer todos los cruces de 3 variables, es decir, x1 * x2 * x3, ya que es probable que explote nuestra cantidad de características.
Así que vamos término por término a través de la expresión lógica, que hará las predicciones correctas para este conjunto de datos de muestra, y averigüe qué pesos necesitarán nuestras neuronas. Recuerde que la expresión que queremos emular con nuestra red neuronal es
(((x1> 0) & (x2> 0)) o (! (X1> 0) &! (X2> 0))) * 2 -1
Función de activación
Quiero abordar rápidamente la función de activación que utilizaremos para nuestras neuronas, la función Sigmoid. La razón por la que elegimos esto es porque la salida de la función Sigmoid está cerca de las salidas de las puertas lógicas.
Las puertas lógicas dan como resultado 1 o 0 y la función Sigmoid emite ~ 1 o ~ 0 para todos los valores de z donde z no está cerca de 0. ie. | z | >> 0. Esto significa que la función Sigmoid será una buena opción para ayudar a nuestras neuronas a emular las compuertas AND y OR que necesitamos.

Comparación x1> 0
Esta es la parte más interna de nuestra función. Podemos calcular esta expresión con bastante facilidad utilizando una sola neurona y una función de activación sigmoidea.
En este caso, solo habrá una entrada variable para la neurona, x1, y nos gustaría que la neurona genere un valor cercano a 1 si x1 es positivo y da un valor cercano a 0 si x1 es negativo. Aunque no es importante para este problema, digamos que queremos una salida de 0.5 si x1 es exactamente cero.
Tenemos la entrada a la función de activación de z = w1 * x1 + b1. Al observar la figura de la función Sigmoid anterior, y al pensar en nuestros criterios anteriores, podemos deducir que queremos b = 0 y w1 debería ser un número positivo grande.
De hecho, como w1 va hacia el infinito, la salida de esta neurona se acerca cada vez más a la salida de la comparación lógica x1> 0. Sin embargo, tomemos un valor más moderado y digamos w1 = 10.
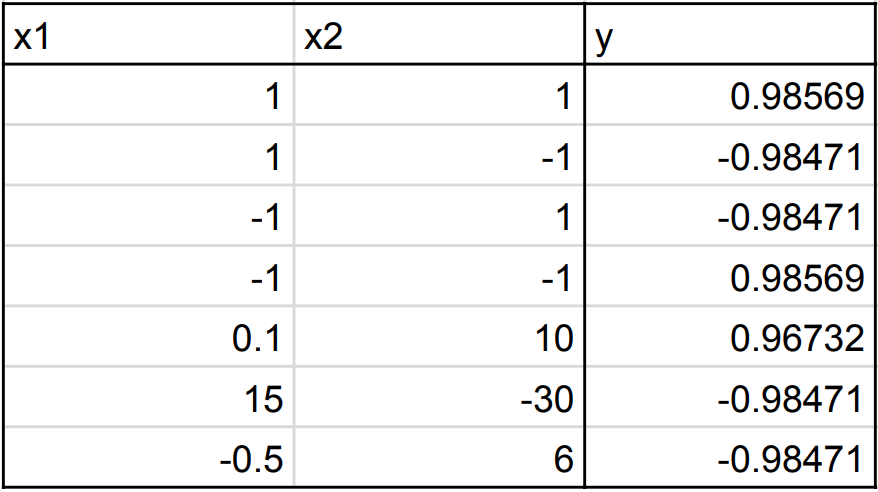
En la siguiente tabla, mostramos el resultado de esta neurona de comparación (columna de la derecha) para diferentes valores de x1 y para w1 = 10. Puedes ver que se comporta muy similar a x1> 0.
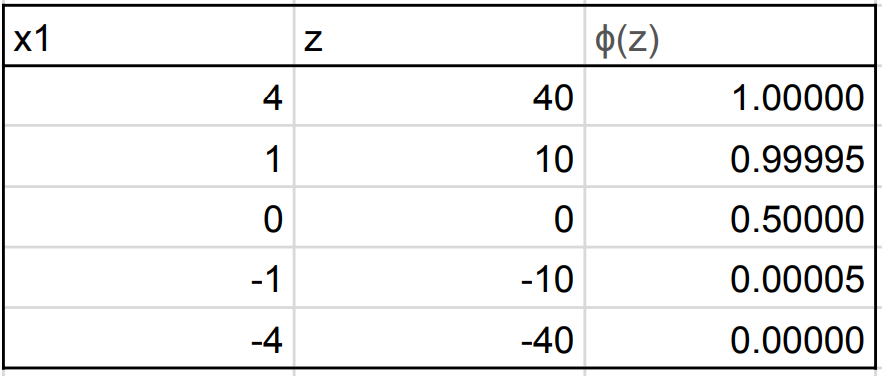
Nota: se puede aplicar la misma lógica para calcular la comparación x2> 0 y establecer w2 = 10 y b2 = 0.
AND Gate
Ahora podemos hacer más que comparaciones, la siguiente función más interna de la expresión lógica de destino es el operador AND. En este caso, la entrada a la función sigmoide será z = w3 * a1 + w4 * a2 + b3. Aquí w3 y w4 son pesos y a1 y a2 son las activaciones de la primera capa de neuronas. La variable a1 está muy cerca de uno si x1> 0 y muy cerca de cero si x1 <0; el valor de a2 es similar.
Para emular el operador Y, nos gustaría establecer los pesos y el sesgo de modo que la salida del Sigmoid sea muy similar a uno si a1 y a2 son ~ 1 y cero en caso contrario.
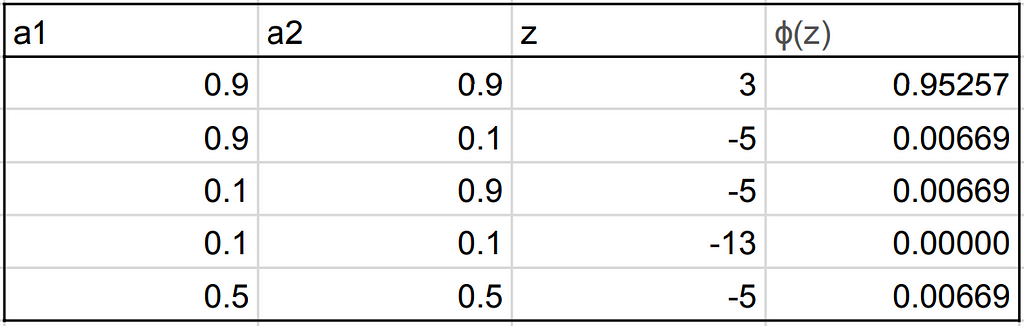
Una buena solución es establecer b3 = -3 / 2 * w3 y w4 = w3. Puede hacer algunos cálculos usted mismo, y ver cómo esta elección en pesos cumplirá nuestros criterios (también hay algunos ejemplos a continuación). Como w3 va al infinito y w4 y b3 van a sus límites correspondientes, esta neurona se vuelve cada vez más como una puerta AND perfecta. Sin embargo, elegiremos un valor más moderado de w3 = 10 y dejaremos que b3 y w4 sigan.
En la siguiente tabla, mostramos el resultado de esta neurona Y (columna de la derecha) para diferentes valores de a1 y a2 y para w1 = 10. Puede ver que se comporta de forma muy similar a una puerta AND.
O Puerta
La siguiente parte más interna de nuestra expresión lógica es la puerta OR. Para una puerta OR, queremos que la salida esté cerca de 1 cuando una o más de las entradas es ~ 1 y cero de lo contrario.
La entrada a la función Sigmoid es z = w7 * a3 + w8 * a4 + b5. Aquí a3 representa si tanto x1 como x2 fueron positivos, y a4 representa si tanto x1 como x2 fueron negativos.
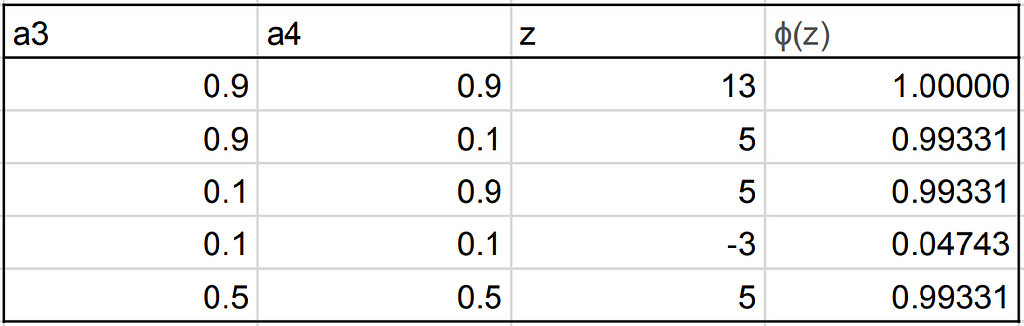
Comparando de nuevo con la función de Sigmoid y considerando los criterios anteriores, deducimos que podemos resolver esto estableciendo b5 = – 1/2 * w7 y w8 = w7.
De nuevo, esto se aproxima a una puerta OR perfecta ya que w1 va al infinito y b5 y w8 van a sus límites correspondientes. Sin embargo. Vamos a elegir un valor modesto de w7 = 10, y dejemos que b5 y w8 sigan.
Pieza final – multiplique y agregue
Para esta parte más externa de nuestra expresión necesitarías multiplicar la salida de tu red neuronal por 2 y restar 1 o bien tener una neurona final con una función de activación lineal y peso w = 2 y sesgo b = -1.
Poniéndolo todo junto
Ahora tenemos todas las piezas que necesitamos para crear nuestro emulador de red neuronal de la expresión lógica anterior. Así que al unir todo, la arquitectura completa de la red se ve así
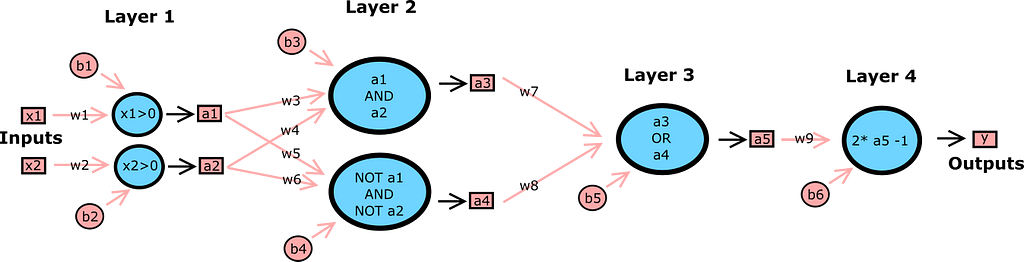
Donde los valores de los pesos y los sesgos son como tales
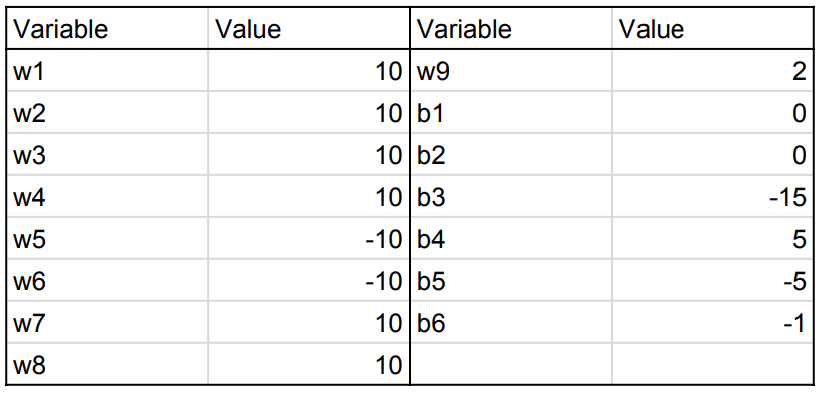
Puede notar que los pesos de los NO a1 Y NO a2 neurona no son las mismas que en la neurona a1 y a2 . Esto se debe a la puerta NOT que no quería empantanar porque no sería divertido volver a ver esta puerta. Sin embargo, puede ser divertido tratar de resolver esto usted mismo.
Usando esta red completa, podemos probar valores de entrada para predecir un valor de salida.
¡Se ve bien! Tiene el resultado que queríamos de la expresión lógica, o al menos está muy cerca.
Capacitación y aprendizaje
Ahora hemos demostrado que esta red neuronal es posible, ahora la pregunta restante es , es posible entrenar. ¿Podemos esperar que si simplemente alimentamos los datos extraídos del gráfico anterior después de definir correctamente las capas, el número de neuronas y las funciones de activación, la red se capacitará de esta manera?
No, no siempre, y ni siquiera a menudo. El problema, como con muchas redes neuronales, es uno de optimización. Al entrenar esta red, a menudo se quedará atrapada en un mínimo local a pesar de que existe una solución casi perfecta.
Aquí es donde su algoritmo de optimización puede desempeñar un papel importante, y esto es algo que Tensorflow Playground no le permite cambiar y puede ser el tema de una publicación futura.
Your Turn
Ahora te recomiendo que vayas a Tensorflow Playground y trates de construir esta red tú mismo, usando la arquitectura (como se muestra en los diagramas arriba y abajo) y los pesos en la tabla de arriba.
El desafío es hacerlo usando solo x1 y x2 como características y para construir la red neuronal manualmente. Tenga en cuenta que debido a las peculiaridades de Tensorflow Playground solo debe agregar las primeras tres capas.
La capa de salida donde ocurre la escala está oscurecida, pero si construyes las primeras tres capas y luego entrena la red por muy poco tiempo, deberías obtener los resultados que se muestran a continuación.
En el patio de recreo puedes editar los pesos haciendo clic en líneas que conectan neuronas. Puede editar los valores de sesgo haciendo clic en los pequeños cuadrados en la esquina inferior izquierda de cada neurona. Debería poder lograr una pérdida de 0.000. Recuerde establecer su función de activación en Sigmoid.
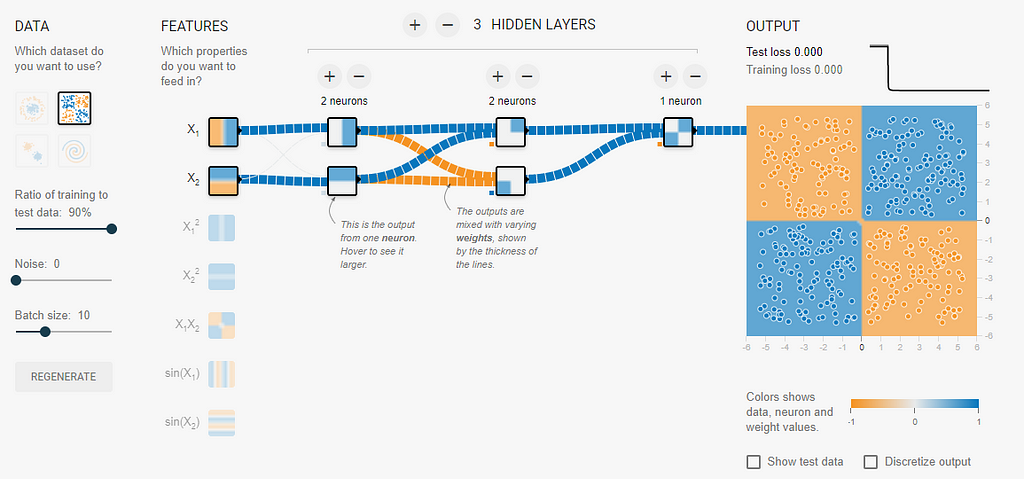
Ideas:
- Después de haber construido esta red ingresando manualmente los pesos, ¿por qué no intentar entrenar los pesos de esta red desde cero en lugar de construirlos manualmente? He logrado hacer esto después de muchas pruebas, pero creo que es bastante sensible a la siembra y, a menudo termina en mínimos locales. Si encuentra una forma confiable de capacitar a esta red usando estas características y esta estructura de red, comuníquese con los comentarios.
- Trate de construir esta red utilizando solo este número de neuronas y capas. En este artículo, he demostrado que es posible hacerlo solo con muchas neuronas. Si introduce más nodos, seguramente tendrá algunas neuronas redundantes. Aunque, con más neuronas / capas, he tenido más suerte en entrenar un buen modelo de forma más consistente.
- Te he mostrado los pesos y los sesgos necesarios para las dos puertas lógicas y una comparación, ¿puedes encontrar los pesos y sesgos? para las otras puertas lógicas en la mesa? Particularmente, la puerta NAND (NOT AND), que es una puerta universal, es decir. si una neurona puede implementar esta puerta (o una aproximación), entonces eso prueba que una red neuronal es capaz de cualquier tarea computacional.
Próxima vez
Espero que hayan disfrutado leyendo este artículo como y la experimento en el patio de recreo tanto como disfruté descubriéndolo.
Tengo ideas para extender esta demostración aún más al producir un cuaderno Jupyter para implementar algo similar en Keras. Entonces usted puede jugar con el entrenamiento de emuladores de puerta lógica de red neuronal usted mismo.