Hay cientos de tipos de GAN. ¿Cómo funciona una función objetivo en cómo se ve una GAN?

Si aún no lo has hecho, definitivamente deberías leer mi publicación previa sobre lo que es una GAN (especialmente si no sabes qué Quiero decir cuando digo GAN!). Esa publicación debería darte un punto de partida para sumergirte en el mundo de los GAN y cómo funcionan. Es una cartilla sólida para cualquier artículo sobre GANs, sin mencionar esta, donde discutiremos funciones objetivas de GANs y otras variaciones de GANs actualmente que usan giros en la definición de sus objetivos para diferentes resultados.
No tiene hora de leer todo? Aquí está el TL; DR
Definición de un objetivo
En nuestra publicación introductoria, hablamos sobre modelos generativos. Discutimos cómo el objetivo de un modelo generativo es encontrar una forma de combinar su distribución generada con una distribución de datos real. Minimizar la distancia entre las dos distribuciones es fundamental para crear un sistema que genere contenido que se vea bien, nuevo y similar a la distribución de datos original.
Pero ¿cómo medimos la diferencia entre nuestra distribución de datos generados y nuestro original? distribución de datos? Eso es lo que llamamos una función objetivo y este es el enfoque de este artículo de hoy. Vamos a ver algunas variaciones de GAN para entender cómo podemos alterar la medida de la divergencia entre nuestra distribución de datos generados y la distribución real y el efecto que eso tendrá.
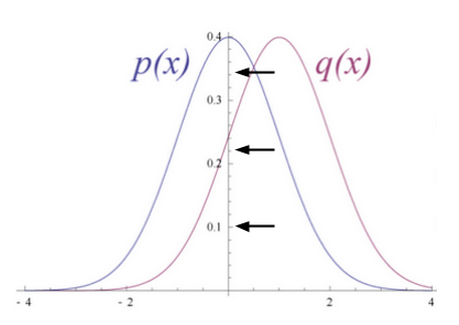
La GAN original [19659005] La función objetivo de nuestro GAN original es esencialmente la minimización de algo llamado Jensen Shannon Divergence (JSD). Específicamente es:
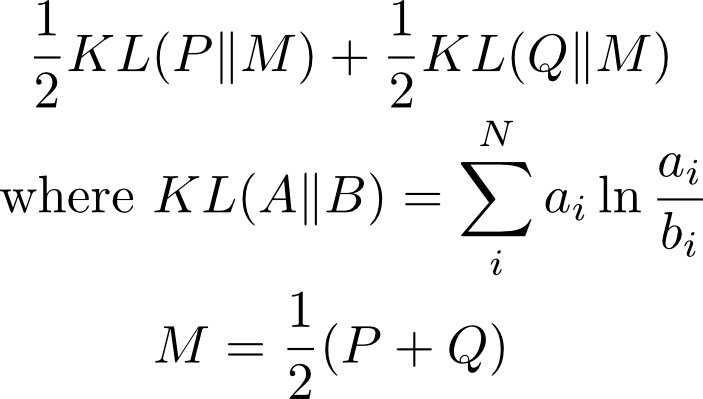
La JSD se deriva de la Kullbach-Liebler Divergence (KLD) que mencionamos en la publicación anterior.
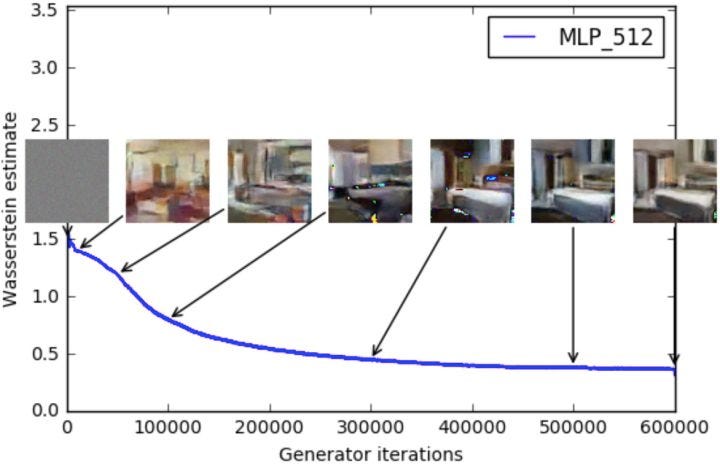
Ya estamos familiarizados con nuestro amigo , el GAN original. En lugar de discutirlo más, admiremos su desempeño en todo su esplendor:

Wasserstein GAN
El Wasserstein GAN (WGAN) es un GAN que puede haber escuchado aproximadamente, ya que recibió mucha atención. Lo hizo por muchas razones prácticas (en general, cuando entrena un GAN, los valores de pérdida devueltos no significan nada excepto que con WGAN pueden), pero ¿qué hizo que WGAN fuera diferente?
WGAN no usa el JSD para medir la divergencia, en su lugar usa algo llamado Distancia de movimiento de tierra (EM) (AKA Wasserstein distance ). La distancia EM se define como:

¿Qué significa esto?
Distancia EM
Probemos y comprendamos la intuición detrás de la distancia EM. Una distribución de probabilidad es esencialmente una colección de masa, y la distribución mide la cantidad de masa en un punto dado. Le damos a EM distancia dos distribuciones. Como el costo de mover una masa a cierta distancia es equivalente al producto de la masa y la distancia, la distancia EM básicamente calcula el costo mínimo de transformar una distribución de probabilidad en la otra. Esto se puede ver como el mínimo esfuerzo necesario.
Pero, ¿por qué nos importa? Bueno, nos importa la distancia EM porque a menudo mide una distancia de una línea recta para transformar una distribución en la otra. Esto es útil con gradientes en optimización. Sin mencionar que también hay un conjunto de funciones que no convergen cuando la distancia se mide con algo como KLD o JSD que realmente convergen para la distancia EM.
Esto se debe a que la distancia EM tiene garantías de continuidad y diferenciabilidad, algo que las funciones de distancia como KLD y JSD carecen. Queremos estas garantías para una función de pérdida, haciendo que la distancia EM se ajuste mejor a nuestras necesidades. Más que eso, todo lo que converge bajo JSD o KLD también converge bajo la distancia EM. Es solo que la distancia EM abarca mucho más.
¿Cómo se usa esto?
Al alejarse de todos estos pensamientos sobre las matemáticas y la aplicación práctica de tales cosas, ¿cómo usamos esta nueva distancia cuando no podemos calcularlo directamente? Bueno, primero tomamos una función crítica que está parametrizada y la capacitamos para aproximar la distancia EM entre nuestra distribución de datos y nuestra distribución generada. Cuando lo hemos logrado, tenemos un buen aproximador para la distancia EM. A partir de ahí, optimizamos nuestra función de generador para reducir esta distancia de EM.
Para garantizar que nuestra función se encuentre en un espacio compacto (esto ayuda a garantizar que cumplamos con las garantías teóricas necesarias para nuestros cálculos), recortamos el ponderaciones que parametrizan nuestra función crítica f.
Solo una nota al margen: nuestra función crítica f se llama crítico porque no es un discriminador explícito. Un discriminador clasificará sus entradas como reales o falsas. El crítico no hace eso. La función crítica solo se aproxima a una puntuación de distancia. Sin embargo, desempeña el papel de discriminador en el marco GAN tradicional, por lo que vale la pena destacar cómo es similar y cómo es diferente.
Key Take-Aways
- Función de pérdida significativa
- Depuración más fácil
- Búsqueda más sencilla de hiperparescopios
- Estabilidad mejorada
- Colapso en modo menos (cuando un generador genera una cosa una y otra vez … Más sobre esto más adelante)
- Garantías de optimización teórica
WGAN mejorado
Con todas esas cosas buenas propuestas con WGAN, ¿qué hay que mejorar? Bueno, La mejor capacitación de Wasserstein GANs resalta eso.
WGAN llamó mucho la atención, la gente comenzó a usarlo y los beneficios estaban ahí. Pero la gente comenzó a notar que a pesar de todas las cosas que WGAN trajo a la mesa, todavía no puede converger o producir muestras generadas bastante malas. El razonamiento que mejora WGAN es que el recorte de peso es un problema. Hace más daño que bien en algunas situaciones. Notamos que la razón por la que grapamos tiene que ver con mantener las garantías teóricas de la función crítica. Pero en la práctica, lo que realmente hace el recorte es fomentar funciones críticas muy simples que se llevan al extremo de sus límites. Esto no es bueno.
Lo que mejor propone WGAN es que no recortes pesos, sino que agregas un término de penalización a la norma del gradiente de la función crítica. Descubrieron que esto produce mejores resultados y, cuando se conectan a un conjunto de arquitecturas GAN diferentes, produce un entrenamiento estable.

Adquisiciones clave
- Exactamente WGAN, excepto que no hay recorte de peso
- término de regularización para alentar garantías teóricas
Mínimos cuadrados GAN
LSGAN tiene una configuración similar a la de WGAN. Sin embargo, en lugar de aprender una función crítica, LSGAN aprende una función de pérdida. La pérdida para muestras reales debe ser menor que la pérdida para muestras falsas. Esto permite al LSGAN enfocarse mucho en muestras falsas que tienen un margen realmente alto.
Al igual que WGAN, LSGAN intenta restringir el dominio de su función. Toman un enfoque diferente en lugar de recorte. Introducen la regularización en forma de disminución de peso, fomentando que los pesos de su función se encuentren dentro de un área limitada que garantice las necesidades teóricas.
Otro punto a tener en cuenta es que la función de pérdida se configura de manera más similar a la GAN original, pero donde el GAN original utiliza una pérdida de registro, el LSGAN utiliza una pérdida L2 (lo que equivale a minimizar la divergencia de Pearson X²). La razón de esto tiene que ver con el hecho de que una pérdida de registro básicamente solo se preocupará de si una muestra está etiquetada correctamente o no. No penalizará fuertemente en función de la distancia de dicha muestra a la clasificación correcta. Si una etiqueta es correcta, no se preocupa más por ella. Por el contrario, la pérdida de L2 se preocupa por la distancia. Los datos que estén lejos de donde deberían estar serán penalizados proporcionalmente. Lo que LSGAN argumenta es que esto produce gradientes más informativos.
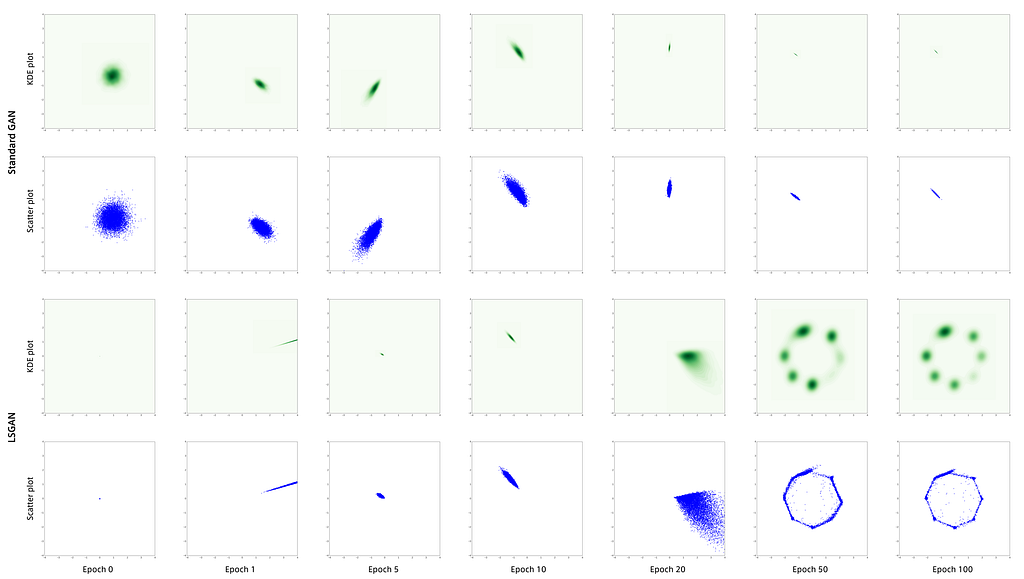
Key Take-Aways
- Función de pérdida en lugar de crítica
- Regularización de pérdida de peso a función de pérdida vinculada
- Pérdida de L2 en lugar de registro pérdida por penalización proporcional
Wasserstein GAN relajado
O RWGAN para abreviar es otra variación del documento de WGAN. Describen su RWGAN como el medio feliz entre WGAN y WGAN mejorado (WGAN-GP como lo citan en el documento). En lugar de una fijación simétrica de pesos (como en WGAN) o una penalización de degradado (como la propuesta para WGAN Mejorado), RWGAN utiliza una estrategia de fijación asimétrica.
Más allá de la arquitectura GAN específica que presentan, también describen lo que llaman una clase estadística de divergencias (denominadas divergencias Wasserstein relajadas o divergencias RW). Las divergencias de RW toman la divergencia de Wasserstein del documento de WGAN y la hacen más general, delineando algunas propiedades probabilísticas clave que son necesarias para mantener algunas de las garantías teóricas de nuestras GAN.
Muestran específicamente que RWGAN parametrizado con divergencia de KL es extremadamente competitivo frente a otros GAN de última generación, pero con mejores propiedades de convergencia que incluso el WGAN regular. También abren su marco para definir nuevas funciones de pérdida y, por lo tanto, nuevas funciones de costos para diseñar un esquema GAN.

Key-Take away
- Pinzamiento asimétrico de pesas
- General RW divergence framework, excelente para el diseño de nuevas funciones de esquema, costos y pérdidas de GAN
McGAN
La Coincidencia de características de media y covarianza GAN (McGAN) es parte de la misma familia de GAN que WGAN. Esta familia recibe el nombre de familia de métrica de probabilidad integral (Integrated Probability Metric, IPM). Estas GAN son las que usan una arquitectura crítica en lugar de un discriminador explícito.
La función crítica para McGAN tiene que ver con medir las características de media o covarianza de la distribución de datos generados y la distribución de datos objetivo. Esto parece bastante sencillo al mirar el nombre también. Definen dos formas diferentes de crear una función crítica, una para la media y otra para la covarianza y demuestran cómo usarlas realmente. Al igual que WGAN, también usan clipping en su modelo, lo que termina restringiendo la capacidad del modelo. No se extrajeron conclusiones súper azarosas de este documento.
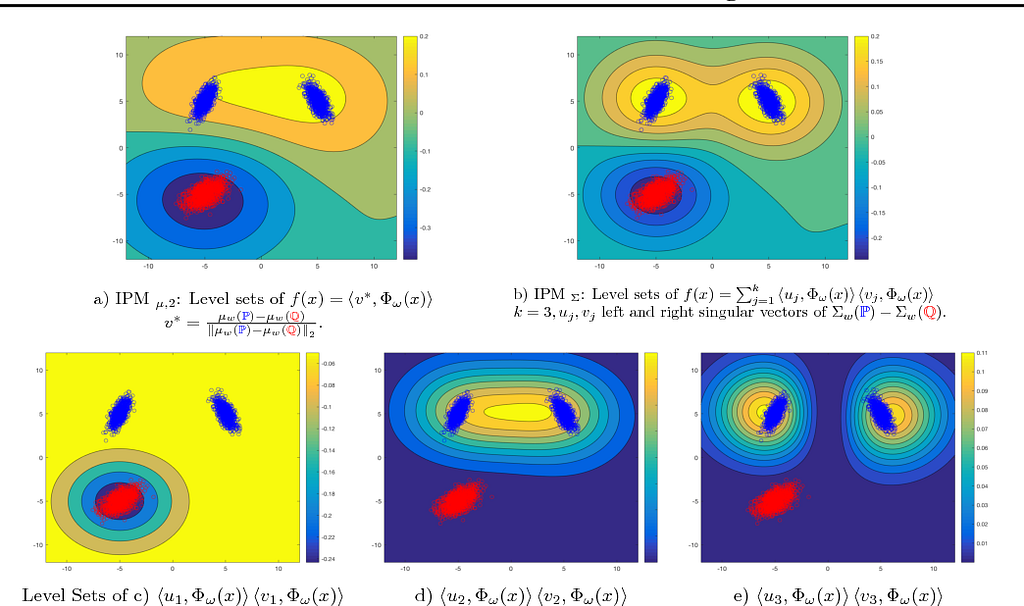
Key-Take-away
- Medida de media y covarianza de la distancia para una función crítica
Redes de coincidencia del momento generador
Momento generativo Matching Networks (GMMN) se centra en minimizar algo llamado máxima discrepancia media (MMD). MMD es esencialmente la media del espacio de incrustación de dos distribuciones, y estamos tratando de minimizar la diferencia entre los dos medios aquí. Podemos usar algo llamado kernel trick que nos permite hacer trampas y usar un kernel gaussiano para calcular esta distancia.
Argumentan que esto permite un objetivo simple que puede ser fácilmente entrenado con la retropropagación, y produce resultados competitivos con un GAN estándar. También mostraron cómo se podía agregar un autocoder en la arquitectura de este GAN para facilitar la capacitación necesaria para estimar con exactitud el MMD.
Una nota adicional: aunque afirman que los resultados de la competencia son los que he leído en otros lugares , parece que sus resultados empíricos a menudo faltan. Además, este modelo es bastante computacionalmente pesado, por lo que el recurso computacional y la compensación de rendimiento realmente no parecen estar ahí en mi opinión.

Key Take-Aways
- Utiliza la máxima discrepancia de medias (MMD) como función de distancia / objetivo
- Sin discriminador, solo mide la distancia entre muestras
- Agrega un auto-codificador para ayudar a medir el MMD
MMD GAN
Discrepancia media máxima GAN o MMD GAN es, lo adivinaste, una mejora de GMMN. Sus principales contribuciones vienen en la forma de no usar núcleos gaussianos estáticos para calcular el MMD, y en su lugar usan técnicas contradictorias para aprender kernels. Combina ideas de los documentos originales GAN y GMMN para crear un híbrido de las ideas de los dos. Los beneficios que alega son un aumento en el rendimiento y el tiempo de ejecución.
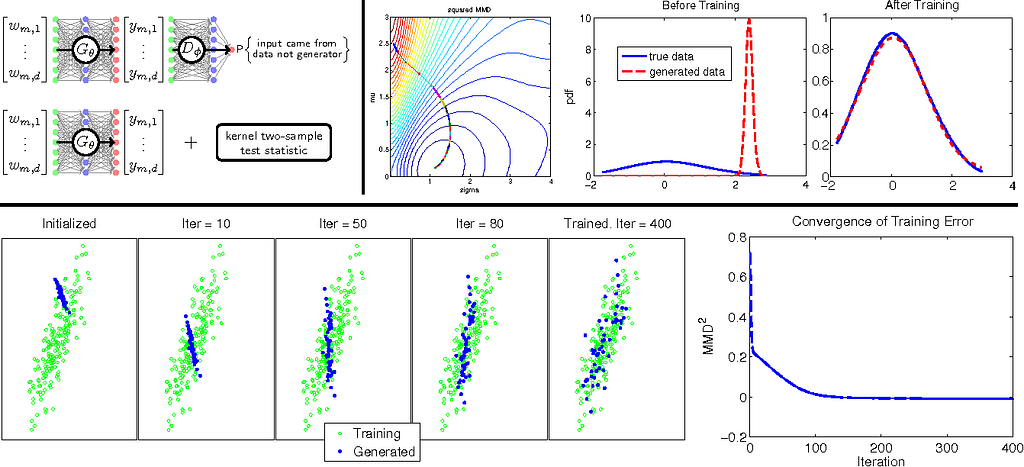
Key Take-Aways
- Iteración en GMMN: Números aprendidos de adversarios para estimar MMD
Cramer GAN
Cramer GAN comienza por delinear un problema con el popular WGAN. Afirma que hay tres propiedades que una divergencia de probabilidad debería satisfacer:
- Invarianza de suma
- Sensibilidad de escala
- Gradientes de muestra imparciales
De estas propiedades, argumentan que la distancia de Wasserstein carece de la propiedad final, a diferencia de KLD o JSD que ambos lo tienen. Demuestran que esto es realmente un problema en la práctica, y proponen una nueva distancia: la distancia de Cramer.
La distancia de Cramer
Ahora, si miramos la distancia de Cramer, podemos ver que se parece un poco al EM distancia. Sin embargo, debido a sus diferencias matemáticas, en realidad no sufre los gradientes de muestra sesgados que tendrá la distancia EM. Esto se demuestra en el documento, si realmente desea profundizar en las matemáticas.

Key Take-Aways
- Distancia de Cramer en lugar de EM distance
- Mejora sobre WGAN: gradientes de muestra no sesgados
Fisher GAN
El Fisher GAN es otra iteración sobre IPM GAN que pretende superar a McGAN, WGAN y WGAN mejorado en una serie de aspectos. Lo que hace es establecer su función objetivo para tener un crítico que tiene una restricción dependiente de datos en su momento de segundo orden (AKA es su varianza).
Debido a este objetivo, Fisher GAN cuenta con lo siguiente:
- Estabilidad de entrenamiento [19659030] Capacidad no restringida
- Computación eficiente
¿Qué hace que la distancia de Fisher GAN sea diferente? Tiene que ver con el hecho de que es esencialmente medir lo que se llama la distancia Mahalanobis que en términos simples es la distancia entre dos puntos que tienen variables correlacionadas, en relación con un centroide que se cree que es la media de la distribución de los datos multivariantes. Esto en realidad asegura que el generador y el crítico estarán limitados como deseamos. A medida que la crítica parametrizada se acerca a la capacidad infinita, en realidad estima la distancia Chi-cuadrado.
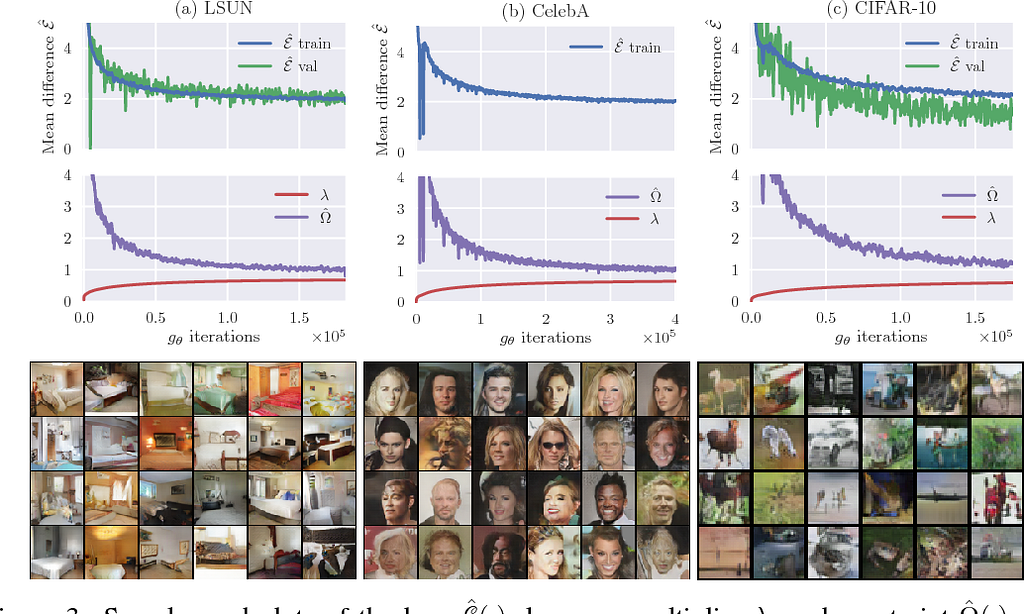
Key Take-Aways
- Mejora por encima de WGAN y otras IPM GAN
- Ofrece estabilidad de entrenamiento, capacidad no restringida y tiempo de cálculo eficiente
- Objetivo de distancia Chi-cuadrado
GAN basado en energía
GAN basado en energía (EBGAN) es uno interesante en nuestra colección de GAN aquí hoy. En lugar de usar un discriminador como el GAN original, usa un autoencoder para calcular la pérdida de reconstrucción. Los pasos para configurar esto:
- Entrenar un autoencoder en los datos originales
- Ahora ejecute imágenes generadas a través de este autoencoder
- Las imágenes mal generadas tendrán una tremenda pérdida de reconstrucción, y por lo tanto esto ahora se convierte en una buena medida
Este es un enfoque realmente genial para configurar el GAN, y con la regularización correcta para evitar el colapso del modo (el generador solo produce la misma muestra una y otra vez), parece ser bastante decente.
Entonces, ¿por qué hacer esto? ? Bueno, lo que se demostró empíricamente es que el uso del autoencoder de esta manera produce una GAN que es rápida, estable y robusta a los cambios de parámetros. Lo que es más, no hay necesidad de intentar y tirar un montón de trucos para equilibrar el entrenamiento del discriminador y el generador.

Key Take-Aways
- Autoencoder como el discriminador
- Reconstrucción pérdida utilizada como costo, configuración similar al costo GAN original
- Rápida, estable y robusta
Equilibrio de límites GAN
Equilibrio de límites GAN (BEGAN) es una iteración en EBGAN. En su lugar, utiliza la pérdida de reconstrucción del autoencoder de una manera similar a la función de pérdida de WGAN.
Para hacer esto, se debe introducir un parámetro para equilibrar el entrenamiento del discriminador y el generador. Este parámetro se pondera como una media móvil sobre las muestras, bailando en el límite entre la mejora de las dos mitades (de ahí su nombre: “equilibrio de límites”).

Key Take-Aways
- Iteration del EBGAN
- Semejanza superficial de la función de costo para WGAN
Adaptación del margen GAN
Adaptación del margen GAN (MAGAN) es el último en nuestra lista. Es otra variación de EBGAN. EBGAN tiene un margen como parte de su función de pérdida para producir una pérdida de bisagra. Lo que hace MAGAN es reducir ese margen monótonamente con el tiempo, en lugar de mantenerlo constante. El resultado de esto es que el discriminador autoencodificará muestras reales mejor.
El resultado que nos importa: mejores muestras y más estabilidad en el entrenamiento.

Key Take-Aways
- Iteración en EBGAN [19659030] Margen de adaptación en la pérdida de la bisagra
- Más estabilidad, mejor calidad
Envolvimiento
¡Fueron muchos GAN diferentes! ¡Y mucho contenido! Creo que vale la pena resumir en una tabla solo para mantenernos organizados:

Vaya … Patémonos en la parte de atrás, eso fue un montón de contenido GAN.
Si me perdí algo o malinterpreté algo, ¡por favor corríjanme! [19659003] Si disfrutaste este artículo o encontraste útil de alguna manera, te amaría por siempre si me dieras un dólar o dos para ayudarme a financiar mi educación e investigación de aprendizaje automático. Cada dólar me ayuda a acercarme un poco más y estoy eternamente agradecido.
¡Y estad atentos para más blogs de GAN en el futuro cercano!
Publicado originalmente en hunterheidenreich.com . [19659140] GAN Objective Functions: GANs and Their Variations se publicó originalmente en Towards Data Science en Medium, donde las personas continúan la conversación resaltando y respondiendo a esta historia.
