Marco teórico
Como sabemos, el árbol nos ha sido útil en muchas formas diferentes, pero en los últimos tiempos, su estructura nos ha inspirado para un algoritmo para resolver problemas y hacer una máquina aprende cosas que queremos que aprendan. Sí, estoy hablando sobre “Algoritmo basado en árboles“.
Los algoritmos de aprendizaje basados en árboles se consideran uno de los mejores y más utilizados métodos de aprendizaje supervisado. Los métodos basados en árboles potencian los modelos predictivos con alta precisión, estabilidad y facilidad de interpretación.
A diferencia de los modelos lineales, mapean bastante bien las relaciones no lineales. Son adaptables para resolver cualquier tipo de problema (clasificación o regresión).
Métodos como árboles de decisión (decision trees), bosque aleatorio (random forest), aumento de gradiente se utilizan popularmente en todo tipo de problemas de ciencia de datos. Por lo tanto, para cada analista es importante aprender estos algoritmos y usarlos para modelar.
Este tutorial está destinado a ayudar a los principiantes a aprender “Algoritmo de árbol de decisión en Machine Learning“, que es el trampolín para aprender modelado basado en árboles, desde cero.
Después de completar con éxito este tutorial, se espera que uno domine el uso del Algoritmo del árbol de decisión en Machine Learning y cree modelos predictivos. Esta publicación cubrirá todo lo que necesita para comenzar.
Introducción
Como gerente de marketing, desea un conjunto de clientes con más probabilidades de comprar su producto. Así es como puede ahorrar su presupuesto de marketing al encontrar su audiencia.
Como administrador de préstamos, debe identificar las solicitudes de préstamos riesgosas para lograr una tasa de incumplimiento de préstamo más baja.
Este proceso de clasificar a los clientes en un grupo de clientes potenciales y no potenciales o solicitudes de préstamos seguros o riesgosos se conoce como un problema de clasificación.
La clasificación es un proceso de dos pasos, paso de aprendizaje y paso de predicción. En el paso de aprendizaje, el modelo se desarrolla en base a datos de capacitación dados.
En el paso de predicción, el modelo se usa para predecir la respuesta para datos dados. El Árbol de decisión en Machine Learning es uno de los algoritmos de clasificación más fáciles y populares de entender e interpretar.
Para la parte práctica de este tema, puede leerlo en esta publicación .
Árboles de decisión puede utilizarse para problemas de clasificación y regresión.
Problemas de tipo regresión
Los problemas de tipo regresión son generalmente aquellos en los que intentamos predecir los valores de una variable continua a partir de una o más variables predictoras categóricas .
Por ejemplo, podemos querer predecir los precios de venta de casas unifamiliares (una variable dependiente continua) a partir de varios otros predictores continuos (p. Ej., Pies cuadrados) así como predictores categóricos (por ejemplo, estilo de hogar, como rancho, dos pisos, etc., código postal o código de área telefónica donde se encuentra la propiedad, etc., tenga en cuenta que esta última variable sería de naturaleza categórica, aunque contendría datos numéricos valores o códigos).
Si utilizamos la regresión múltiple simple, o algún modelo lineal general (GLM) para predecir los precios de venta de viviendas unifamiliares, determinaríamos una ecuación lineal para estas variables que puede usarse para calcular los precios de venta pronosticados
Problemas de tipo de clasificación
Los problemas de tipo de clasificación generalmente son aquellos en los que intentamos predecir los valores de una variable dependiente categórica (clase, pertenencia a grupos, etc.) a partir de una o más variables predictoras continuas y / o .
Por ejemplo, podemos estar interesados en predecir quién se graduará o no de la universidad, o quién renovará o no una suscripción. Estos serían ejemplos de problemas simples de clasificación binaria, donde la variable dependiente categórica solo puede asumir dos valores distintos y mutuamente excluyentes.
En otros casos, podríamos estar interesados en predecir cuál de los múltiples productos de consumo alternativos diferentes (por ejemplo, marcas de automóviles) decide comprar una persona, o qué tipo de falla ocurre con diferentes tipos de motores. En esos casos, existen múltiples categorías o clases para la variable dependiente categórica.

Qué es el algoritmo del árbol de decisión en Machine Learning?
Un árbol de decisión en Machine Learning es una estructura de árbol similar a un diagrama de flujo donde un nodo interno representa una característica (o atributo), la rama representa una regla de decisión y cada nodo hoja representa el resultado.
El nodo superior en un árbol de decisión en Machine Learning se conoce como el nodo raíz. Aprende a particionar en función del valor del atributo. Divide el árbol de una manera recursiva llamada partición recursiva.
Esta estructura tipo diagrama de flujo lo ayuda a tomar decisiones. Es una visualización como un diagrama de flujo que imita fácilmente el pensamiento a nivel humano. Es por eso que los árboles de decisión son fáciles de entender e interpretar.
Los árboles de decisión clasifican los ejemplos clasificándolos por el árbol desde la raíz hasta algún nodo hoja, con el nodo hoja proporcionando la clasificación al ejemplo, este enfoque se llama Enfoque de arriba hacia abajo.
Cada nodo en el árbol actúa como un caso de prueba para algún atributo, y cada borde que desciende de ese nodo corresponde a una de las posibles respuestas al caso de prueba. Este proceso es recursivo y se repite para cada subárbol enraizado en los nuevos nodos.

Antes de profundizar, familiarícese con algunas de las terminologías:
- Nodo raíz (nodo de decisión superior ): Representa a toda la población o muestra y esto se divide en dos o más conjuntos homogéneos.
- División: Es un proceso de división de un nodo en dos o más subnodos.
- Nodo de decisión: Cuando un subnodo se divide en subnodos adicionales, se llama nodo de decisión.
- Nodo de hoja / terminal: Los nodos sin hijos (sin división adicional) se llaman Hoja o nodo terminal.
- Poda: Cuando reducimos el tamaño de los árboles de decisión eliminando nodos (opuesto a la división), el proceso se llama poda.
- Rama / Subárbol: Una subsección del árbol de decisión se denomina rama o subárbol.
- Nodo padre e hijo: Un nodo, que se divide en subnodos se denomina nodo principal de subnodos, mientras que los subnodos son hijos de un nodo principal.
¿Cómo funciona el algoritmo del árbol de decisión en Machine Learning?
La idea básica detrás de cualquier algoritmo de árbol de decisión es el siguiente:
- Seleccione el mejor atributo utilizando Medidas de selección de atributos (ASM) para dividir los registros.
- Haga que ese atributo sea un nodo de decisión y divida el conjunto de datos en subconjuntos más pequeños. recursivamente para cada hijo hasta que una de las condiciones coincida:
- Todas las tuplas pertenecen al mismo valor de atributo.
- No quedan más atributos.
- No hay más instancias.

La matemática detrás de los árboles de decisión en Machine Learning
Medidas de selección de atributos
La medida de selección de atributos es una heurística para seleccionar el criterio de división que divide los datos de la mejor manera posible. También se conoce como reglas de división porque nos ayuda a determinar puntos de interrupción para tuplas en un nodo dado.
ASM proporciona un rango para cada característica (o atributo) al explicar el conjunto de datos dado. El atributo de mejor puntuación se seleccionará como un atributo de división ( Fuente ).
En el caso de un atributo de valor continuo, los puntos de división para las ramas también deben definirse. Las medidas de selección más populares son Ganancia de información, Proporción de ganancia e Índice de Gini.
1. Ganancia de información:
La ganancia de información es una propiedad estadística que mide qué tan bien un atributo dado separa los ejemplos de entrenamiento de acuerdo con sus clasificación objetivo.
Mire la imagen a continuación y piense qué nodo se puede describir fácilmente. Estoy seguro de que su respuesta es C porque requiere menos información ya que todos los valores son similares.
Por otro lado, B requiere más información para describirlo y A requiere la información máxima. En otras palabras, podemos decir que C es un nodo puro, B es menos impuro y A es más impuro.

Ahora, podemos llegar a la conclusión de que un nodo menos impuro requiere menos información para describirlo. Y, el nodo más impuro requiere más información.
En un ejemplo paralelo considerando la ganancia de información, en la figura a continuación, podemos ver que un atributo con baja ganancia de información (abajo) divide los datos de manera relativamente uniforme y como resultado no nos acerque más a una decisión.
Mientras que un atributo con alta ganancia de información (arriba) divide los datos en grupos con un número desigual de positivos y negativos y, como resultado, ayuda a separarlos entre sí.


Para poder calcular la ganancia de información, primero tenemos que introducir el término entropía de un conjunto de datos.
Entropía
Shannon inventó El concepto de entropía, que mide la impureza del conjunto de entrada. En física y matemáticas, la entropía se conoce como aleatoriedad o impureza en el sistema. En teoría de la información, se refiere a la impureza en un grupo de ejemplos. La ganancia de información es una disminución de la entropía.
La idea detrás de la entropía es, en términos simplificados, la siguiente: Imagina que tienes una rueda de lotería que incluye 100 bolas verdes. Se puede decir que el conjunto de bolas dentro de la rueda de lotería es totalmente puro porque solo se incluyen bolas verdes.
Para expresar esto en la terminología de entropía, este conjunto de bolas tiene una entropía de 0 (también podemos decir impureza cero). Considere ahora, 30 de estas bolas son reemplazadas por bolas rojas y 20 por bolas azules.

Si ahora saca otra bola de la rueda de lotería, la probabilidad de recibir una bola verde se ha reducido de 1.0 a 0.5. Como la impureza aumentó, la pureza disminuyó, por lo tanto también aumentó la entropía.
Por lo tanto, podemos decir que cuanto más “impuro” sea un conjunto de datos, mayor será la entropía y menos “impuro” un conjunto de datos, menor será la entropía
Tenga en cuenta que la entropía es 0 si todos los miembros de S pertenecen a la misma clase. Por ejemplo, si todos los miembros son positivos, Entropía (S) = 0.
La entropía es 1 cuando la muestra contiene el mismo número de ejemplos positivos y negativos. Si la muestra contiene un número desigual de ejemplos positivos y negativos, la entropía está entre 0 y 1.
La siguiente figura muestra la forma de la función de entropía en relación con una clasificación booleana, ya que la entropía varía entre 0 y 1.

Se puede calcular la entropía usando la fórmula: –
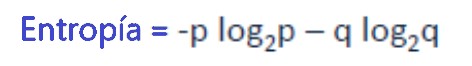
Aquí pyq es la probabilidad de éxito y fracaso respectivamente en ese nodo. La entropía también se usa con la variable objetivo categórica. Elige la división que tiene la entropía más baja en comparación con el nodo principal y otras divisiones. Cuanto menor sea la entropía, mejor será.
La ganancia de información calcula la diferencia entre la entropía antes de la división y la entropía promedio después de la división del conjunto de datos en función de los valores de atributo dados
Ganancia de información = Entropía (nodo padre) – [Avg Entropia(nodo hijo)]
Pasos para calcular la entropía para una división:
- Calcular la entropía del nodo principal
- Calcular la entropía de cada nodo individual de división y calcular el promedio ponderado de todos los subnodos disponibles en una división.
Ejemplo: Digamos que tenemos una muestra de 30 estudiantes con tres variables Sexo (Niño / Niña), Clase (IX / X) y Altura (5 a 6 pies). 15 de estos 30 juegan al cricket en el tiempo libre.
Ahora, quiero crear un modelo para predecir quién jugará al cricket durante un período de ocio. En este problema, necesitamos segregar a los estudiantes que juegan al cricket en su tiempo libre según una variable de entrada altamente significativa entre los tres.

Entropía para el nodo principal = – (15/30) log2 (15/30) – (15 / 30) log2 (15/30) = 1
Aquí 1 muestra que es un nodo impuro.
Para dividir en género:
Entropía para:
- Nodo Femenino = – (2/10 ) log2 (2/10) – (8/10) log2 (8/10) = 0,72
- Nodo Masculino = – (13/20) log2 (13/20) – (7/20) log2 (7/20) = 0.93
- Por División de Género = (10/30) * 0.72 + (20/30) * 0.93 = 0.86
Ganancia de información por división por género = 1–0.86 = 0.14
Para división en clase:
Entropía para:
- Nodo de clase IX = – (6/14) log2 (6/14) – (8/14) log2 (8/14) = 0.99
- Clase Nodo X = – (9/16) log2 (9/16) – (7/16) log2 (7/16) = 0.99
- Por División de Clase = (14/30) * 0.99 + (16/30) * 0.99 = 0.99
Ganancia de información para s plit on Class = 1– 0.99 = 0.01
Arriba, puede ver que la ganancia de información para Split on Gender es la más alta de todas, por lo que el árbol se dividirá en Género .
2. Gini
¿ Qué es el índice de Gini ?
El índice de Gini calcula la cantidad de probabilidad de que una característica específica se clasifique incorrectamente cuando se selecciona al azar.
- Si todos los elementos están vinculados a una sola clase, se llama pura.
- Va de 0-1
- 0 = todos los elementos
- 1 = Distribuido aleatoriamente
- 0,5 = igualmente distribuido
- Significa que se debe preferir un atributo con un índice de Gini más bajo.

Ecuación del índice de Gini:

donde pi es la probabilidad de que un objeto sea clasificado en una clase específica.
Ejemplo de índice de Gini
Ahora entenderemos el índice de Gini usando la siguiente tabla:
Consta de 14 filas y 4 columnas. La tabla muestra en qué factor se produce la enfermedad cardíaca en la variable dependiente de la persona (objetivo) según la presión arterial alta, el colesterol alto y el FBS (azúcar en sangre en ayunas).
Nota: Los valores originales se convierten en 1 y 0, que representan la clasificación numérica.

Gini dice que si seleccionamos dos elementos de una población al azar, entonces deben ser de la misma clase y la probabilidad de esto es 1 si la población es pura.
- Funciona con la variable objetivo categórica “Éxito” o “Fracaso” “.
- Realiza solo divisiones binarias
- Cuanto mayor sea el valor de Gini, mayor será la homogeneidad.
- CART (árbol de clasificación y regresión) utiliza el método Gini para crear divisiones binarias.
Pasos para calcular Gini para una división
- Calcule Gini para sub-nodos, usando la suma de la fórmula del cuadrado de probabilidad de éxito y fracaso (p² + q²).
- Calcule Gini para la división usando la puntuación ponderada de Gini de cada nodo de esa división
Ejemplo: – Refiriéndose al ejemplo utilizado anteriormente, donde queremos segregar a los estudiantes en función de la variable objetivo (jugar cricket o no). En la siguiente instantánea, dividimos la población usando dos variables de entrada de género y clase. Ahora, quiero identificar qué división está produciendo sub-nodos más homogéneos usando Gini.

División por género:
- Calcular, Gini para el sub-nodo Femenino= (0.2) * (0.2) + (0.8 ) * (0.8) = 0.68
- Gini para sub-nodo Masculino = (0.65) * (0.65) + (0.35) * (0.35) = 0.55
- Calcular Gini ponderado para división de Género = (10/30) * 0.68+ (20/30) * 0.55 = 0.59
Similar para División por Clase:
- Gini para sub-nodo Clase IX = (0.43) * (0.43) + (0.57) * (0.57) = 0.51
- Gini para sub-nodo Clase X = (0.56) * (0.56) + (0.44) * (0.44) = 0.51
- Calcular Gini ponderado para división de Clase = (14 /30)*0.51+(16/30)*0.51 = 0.51
Arriba, puede ver que la puntuación de Gini para Dividir en género es mayor que Dividir en Clase, por lo tanto, la división de nodos tendrá lugar en Género.
A menudo se puede encontrar el término ‘Impureza de Gini’ que se determina restando el valor de Gini de 1. En términos generales, podemos decir,
Impureza de Gini = 1-Gini
Gini es el parámetro predeterminado en el Algoritmo del árbol de decisión.
También hay otras medidas, pero sobre todo usará estas dos. Para comprender la implementación del árbol de decisiones con scikit learn y cómo funciona, puede consultar esta publicación .
Gracias por su tiempo y feliz aprendizaje !!! 🙂