A continuación, describiremos el proceso de extracción de picos de redes neuronales python individuales a partir de datos en bruto y su preparación para la clasificación de picos.
Las redes neuronales biológicas, como el cerebro humano, están formadas por células especializadas llamadas neuronas. Existen varios tipos de neuronas pero todas ellas se basan en el mismo concepto. Las moléculas de señalización llamadas neurotransmisores se liberan en la sinapsis, el punto de conexión entre dos neuronas.
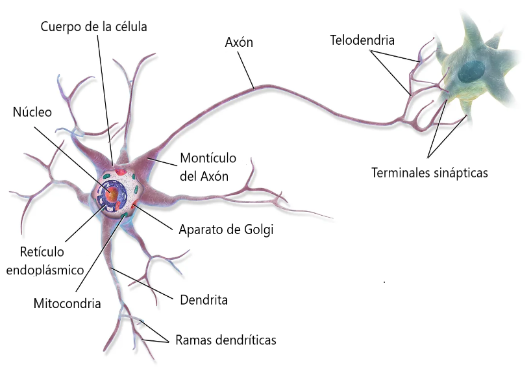
Los neurotransmisores alteran el potencial de membrana de la célula postsináptica al interactuar con los canales iónicos dentro de su membrana celular. Si la despolarización de la célula postsináptica es lo suficientemente fuerte, se genera un potencial de acción en el cono del axón.
El potencial de acción viajará a lo largo del axón y desencadenará la liberación de neurotransmisores en la hendidura sináptica que afectará el potencial de membrana de la siguiente neurona.
De esta manera, se puede transmitir una señal de una célula a otra a través de (completa) la red, siendo el potencial de acción el desencadenante de la liberación de neurotransmisores en la sinapsis.
La comunicación neuronal es de naturaleza electroquímica y saber cuándo y bajo qué condiciones se generan los potenciales de acción puede brindar información valiosa sobre el funcionamiento del cerebro.
Pero estudiar la actividad de las neuronas individuales dentro del cerebro vivo es una tarea desafiante. No existe un método no invasivo disponible a través del cual se pueda monitorear la actividad neuronal en un solo nivel celular en tiempo real.
Por lo general, se inserta un electrodo en el cerebro para registrar la actividad eléctrica en sus inmediaciones. En este tipo de grabaciones electrofisiológicas, un potencial de acción aparece como un pico rápido de gran amplitud.
Pero debido a que las neuronas están empaquetadas densamente dentro del cerebro, un electrodo de registro normalmente recogerá picos neuronales de más de una neurona a la vez.
Entonces, si queremos entender cómo se comportan las neuronas individuales, necesitamos extraer los picos de redes neuronales de la grabación y verificar si fueron generados por una o posiblemente varias neuronas.
La extracción y el agrupamiento de picos de redes neuronales de los datos se conoce como ordenación de picos.
Introducción
Primero, necesitamos datos. Existe un popular algoritmo de clasificación de picos de redes neuronales python disponible para Matlab llamado Wave Clus . En la sección de datos de su página web proporcionan un conjunto de datos de prueba que usaremos aquí.
De acuerdo con la información proporcionada en la página web, la grabación dura aproximadamente 30 minutos y proviene de un paciente con epilepsia.
Los datos se almacenan en un archivo .ncs que es el formato de datos de la empresa que fabricó el sistema de grabación. Entonces, si queremos leer la grabación en Python, necesitamos entender cómo se almacenan los datos.
Hay una descripción detallada sobre el formato de archivo .ncs en la página web de las compañías que podemos usar para importar el archivo:
# Definir ruta de datos data_file = './UCLA_data/CSC4.Ncs';
# El encabezado tiene 16 kilobytes de longitud header_size = 16 * 1024
# Open archivo fid = open(data_file , 'rb')
# Saltear encabezado cambiando la posición por tamaño de encabezado
fid.seek(header_size)
# Leer datos según la información de Neuralynx
data_format = np.dtype ([('TimeStamp' npuint64)
('ChannelNumber', np.uint32),
('SampleFreq', np.uint32),
('NumValidSamples', np. uint32),
('Muestras', np.int16, 512)])
raw = np.fromfile(fid, dtype = data_format)
# Cerrar archivo fid.close()
# Obtener frecuencia de muestreo sf = raw ['SampleFreq'][0]
# Crear vector de datos data = raw ['Samples'].ravel()
Como podemos ver en el código anterior, el archivo .ncs también contiene información adicional sobre la grabación. Lo más importante es la frecuencia de muestreo que nos dice cuántos puntos de datos se registraron por segundo.
Con la frecuencia de muestreo y el número de muestras en los datos, ahora podemos crear un vector de tiempo que nos permite trazar la señal a lo largo del tiempo.
El siguiente código hará esto y trazará el primer segundo de la señal:
# Determine la duración de la grabación en segundos dur_sec = data.shape[0] / sf
# Crear vector de tiempo time = np.linspace (0, dur_sec, data.shape [0])
# Trazar el primer segundo de datos
fig, ax = plt.subplots (figsize = (15, 5))
ax.plot(time [0:sf] data[0:sf])
ax.set_title('Broadband; Frecuencia de muestreo: {} Hz'.format(sf), fontsize = 23)
ax.set_xlim(0, time[sf])
ax.set_xlabel('tiempo[s]', fontsize = 20)
ax.set_ylabel('amplitud[uV]', fontsize = 20)
plt.show()

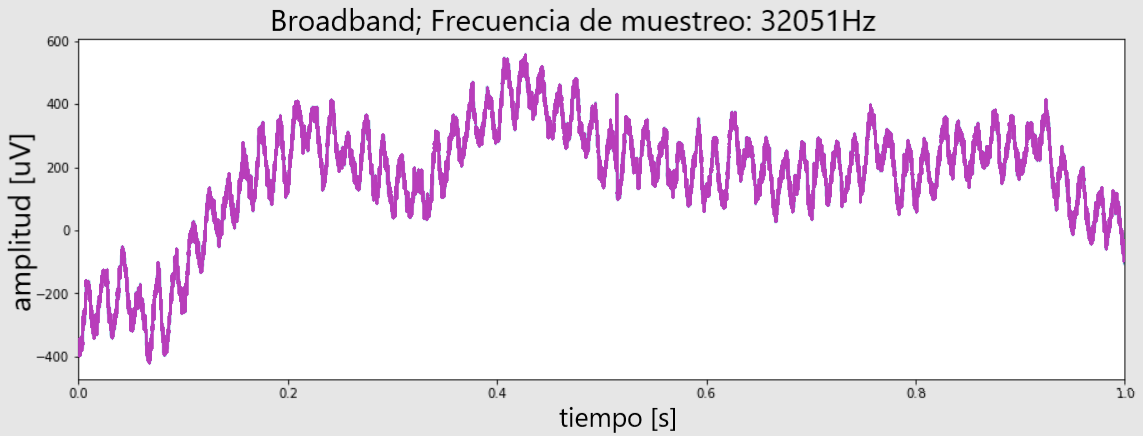
De acuerdo, entonces, ¿vemos picos? … No, no lo hacemos. Pero sí vemos algún tipo de actividad rítmica en los datos. Entonces, ¿es esta una señal significativa? De nuevo, la respuesta es no.
Si tuviéramos que contar el número de picos de redes neuronales en este primer segundo de datos, terminaríamos con un conteo de 60 picos, lo que significa que estamos viendo una oscilación de 60 Hz. Podemos confirmar esto trazando el espectro de potencia de la señal que muestra un pico claro a 60 Hz.
Entonces, ¿qué estamos viendo? En la página web de donde obtuvimos los datos, dice que la grabación proviene del laboratorio de Itzhak Fried en la UCLA en EE. UU.
La frecuencia de la fuente de alimentación en los Estados Unidos es de 60 Hz. Entonces, lo que estamos viendo es en realidad el ruido eléctrico de los dispositivos electrónicos que estaban en la sala durante la recolección de datos.
Encontrando los picos de redes neuronales python en la señal
Aunque hay 60 Hz de ruido en los datos, aún podemos trabajar con eso. Por suerte para nosotros, los potenciales de acción son eventos rápidos que solo duran de 1 a 2 milisegundos.
Entonces, lo que podemos hacer aquí es filtrar la señal de banda ancha bruta en un rango que excluye el ruido de 60 Hz. Una configuración de filtro típica es de 500 a 9000 Hz y nuestra implementación de Python tiene el siguiente aspecto:
# Importar libarys from scipy.signal import butter, lfilter
def filter_data(data, low = 500, high = 9000,sf , orden = 2): # Determinar la frecuencia de Nyquist nyq = sf / 2
# Establecer bandas low = low / nyq high = high / nyq
# Calcular coeficientes b, a = butter(orden, [low, high] btype = 'band')
# Señal de filtro filtered_data = lfilter (b, a, data) return filtered_data El uso de la función anterior nos permite comparar los datos sin procesar con la señal filtrada:
spike_data = filter_data(data, low=500, high=9000, sf=sf) # Plot signals fig, ax = plt.subplots(2, 1, figsize=(15, 5)) ax[0].plot(time[0:sf], data[0:sf]) ax[0].set_xticks([]) ax[0].set_title('Broadband', fontsize=23) ax[0].set_xlim(0, time[sf]) ax[0].set_ylabel('amplitude [uV]', fontsize=16) ax[0].tick_params(labelsize=12) ax[1].plot(time[0:sf], spike_data[0:sf]) ax[1].set_title('Spike channel [0.5 to 9kHz]', fontsize=23) ax[1].set_xlim(0, time[sf]) ax[1].set_xlabel('time [s]', fontsize=20) ax[1].set_ylabel('amplitude [uV]', fontsize=16) ax[1].tick_params(labelsize=12) plt.show()
Procesamiento de la señal los datos con la función anterior nos darán la banda de alta frecuencia, o canal de pico, de la señal. Nuestra expectativa es que este canal de picos de redes neuronales python contengan los potenciales de acción y ya no tenga ruido de 60 Hz.
Así que veamos el canal de pico filtrado y compáralo con la señal de banda ancha en bruto.

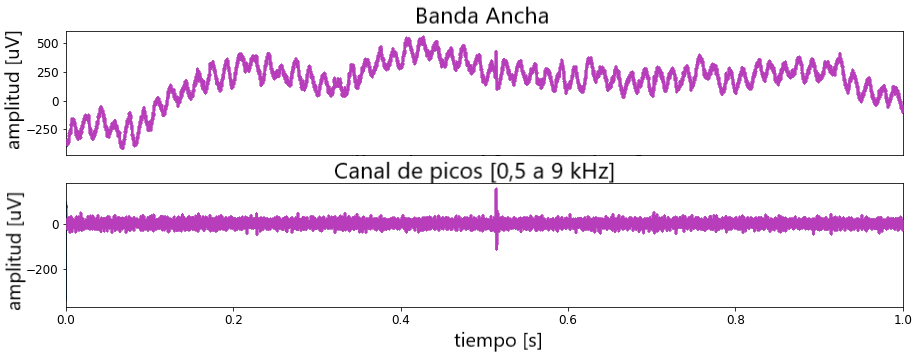
Como era de esperar, el canal de pico ya no muestra ninguna oscilación de 60 Hz. Y lo más importante, finalmente podemos ver el primer pico en la grabación. Alrededor de 0,5 segundos en la grabación es claramente visible en los datos filtrados.
Además, ahora que ahora buscamos, podemos verlo en los datos sin filtrar. Sin embargo, es más difícil de detectar debido al ruido de 60 Hz.
Extracción de picos de redes neuronales python de la señal
Ahora que hemos separado la banda de picos de redes neuronales python de alta frecuencia de la banda de bajas frecuencias ruidosas, podemos extraer los picos individuales. Para esto vamos a escribir una función simple que hace lo siguiente:
- Encontrar puntos de datos en la señal que están por encima de un cierto umbral
- Definir una ventana alrededor de estos eventos y “cortarlos”
- Alíñelos a su amplitud máxima
Además, también definiremos un umbral superior. Los puntos de datos por encima de este umbral serán rechazados ya que son artefactos de alta frecuencia probables.
Dichos artefactos pueden surgir a través de los movimientos del paciente o pueden reflejar eventos eléctricos como encender o apagar una bombilla en la habitación.
Puede obtener una visión detallada de la función de extracción de espigas en Jupyter Notebook . Aquí solo vamos a echar un vistazo a los 100 picos de redes neuronales aleatorios que se extrajeron de la señal con nuestra función.
def get_spikes(data, spike_window=80, tf=5, offset=10, max_thresh=350):
# Calculate threshold based on data mean
thresh = np.mean(np.abs(data)) *tf
# Find positions wherere the threshold is crossed
pos = np.where(data > thresh)[0]
pos = pos[pos > spike_window]
# Extract potential spikes and align them to the maximum
spike_samp = []
wave_form = np.empty([1, spike_window*2])
for i in pos:
if i < data.shape[0] - (spike_window+1):
# Data from position where threshold is crossed to end of window
tmp_waveform = data[i:i+spike_window*2]
# Check if data in window is below upper threshold (artifact rejection)
if np.max(tmp_waveform) < max_thresh: # Find sample with maximum data point in window tmp_samp = np.argmax(tmp_waveform) +i # Re-center window on maximum sample and shift it by offset tmp_waveform = data[tmp_samp-(spike_window-offset):tmp_samp+(spike_window+offset)] # Append data spike_samp = np.append(spike_samp, tmp_samp) wave_form = np.append(wave_form, tmp_waveform.reshape(1, spike_window*2), axis=0) # Remove duplicates ind = np.where(np.diff(spike_samp) > 1)[0]
spike_samp = spike_samp[ind]
wave_form = wave_form[ind]
return spike_samp, wave_form
Usando la función en nuestro canal de picos filtrado y trazando 100 formas de onda seleccionadas al azar que se extrajeron:
spike_samp, wave_form = get_spikes(spike_data, spike_window=50, tf=8, offset=20)
np.random.seed(10)
fig, ax = plt.subplots(figsize=(15, 5))
for i in range(100):
spike = np.random.randint(0, wave_form.shape[0])
ax.plot(wave_form[spike, :])
ax.set_xlim([0, 90])
ax.set_xlabel('# sample', fontsize=20)
ax.set_ylabel('amplitude [uV]', fontsize=20)
ax.set_title('spike waveforms', fontsize=23)
plt.show()
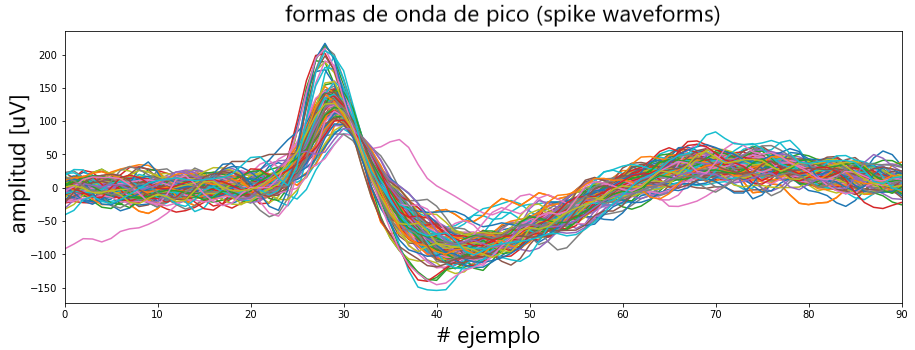
En la gráfica anterior, podemos ver que hay al menos dos tipos de formas de onda en los datos. Un grupo de picos de redes neuronales con un pico agudo de gran amplitud y un segundo grupo con un pico inicial más amplio.
Entonces, lo más probable es que estos picos de redes neuronales hayan sido generados por más de una neurona. La siguiente tarea, por lo tanto, es encontrar una forma de agrupar las formas de onda en diferentes clusters.
Pero como esto no puede ser codificado o explicado en dos o tres líneas, veremos el tema de clasificación de spikes en la próxima publicación.
El código para este proyecto se puede encontrar en Github .