Desafíos en la clasificación y técnicas para mejorar el rendimiento

Los problemas de clasificación multiclase en aprendizaje automático con un conjunto de datos desequilibrado presentan un desafío diferente al de un problema de clasificación binaria.

La distribución sesgada hace que muchos algoritmos convencionales de aprendizaje automático sean menos efectivos, especialmente para predecir ejemplos de clases minoritarias. Para hacerlo, primero comprendamos el problema en cuestión y luego analicemos las formas de superarlo.

1. Clasificación multiclase en aprendizaje automático

Una tarea de clasificación con más de dos clases por ejemplo, clasificar un conjunto de imágenes de frutas que pueden ser naranjas, manzanas o peras.

La clasificación multiclase en aprendizaje automático parte del supuesto de que a cada muestra se le asigna una y sólo una etiqueta: una fruta puede ser una manzana o una pera, pero no ambas al mismo tiempo.

2. Conjunto de datos desequilibrados

Los datos desequilibrados generalmente se refieren a un problema de clasificación donde las clases no están representadas por igual.

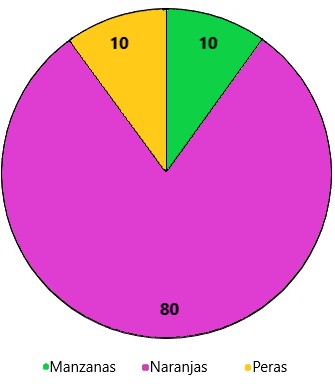
Por ejemplo, es posible que tenga un problema de clasificación de tres clases de un conjunto de frutas para clasificar como naranjas, manzanas o peras con un total de 100 instancias.

Un total de:

• 80 instancias están etiquetadas con Clase-1 (Naranjas).
• 10 instancias con Clase-2 (Manzanas).
• 10 instancias restantes están etiquetadas con Clase-3 (Peras).

Este es un conjunto de datos desequilibrado y la proporción de 8:1:1. La mayoría de los conjuntos de datos de clasificación no tienen exactamente el mismo número de instancias en cada clase.

Pero una pequeña diferencia a menudo no importa. Hay problemas en los que el desequilibrio de clases no sólo es común, sino que se espera. Por ejemplo, en conjuntos de datos como los que caracterizan las transacciones fraudulentas están desequilibrados.

Conjunto de datos

El conjunto de datos que utilizaremos para este ejemplo es el famoso conjunto de datos “20 grupos de noticias” .

El conjunto de datos de 20 grupos de noticias es una colección de aproximadamente 20.000 documentos de grupos de noticias, divididos (casi) uniformemente en 20 grupos de noticias diferentes.

La colección de 20 grupos de noticias se ha convertido en un conjunto de datos popular para experimentos en aplicaciones de texto de técnicas de aprendizaje automático, como la clasificación y agrupación de texto.

scikit-learn proporciona las herramientas para preprocesar el conjunto de datos; consulte aquí para obtener más detalles. El número de artículos para cada grupo de noticias que se indica a continuación es aproximadamente uniforme.

 

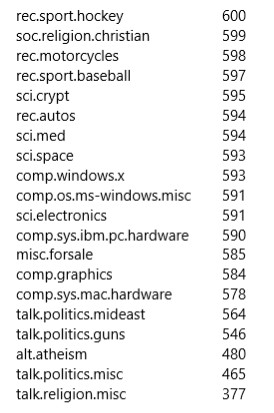
Eliminamos algunos artículos de noticias de algunos grupos para desequilibrar el conjunto de datos general, como se muestra a continuación:

Ahora nuestro conjunto de datos desequilibrado con 20 clases está listo para un análisis más detallado.

Construcción del modelo

Como este es un problema de clasificación, usaremos:

from keras.models import Sequential
from keras.layers import Dense, Embedding, LSTM, GRU
from keras.layers.embeddings import Embedding

EMBEDDING_DIM = 100

print('Build model...')

model = Sequential()
model.add(Embedding(vocab_size, EMBEDDING_DIM, input_length=max_length))
model.add(GRU(units=32, dropout=0.2, recurrent_dropout=0.2))
model.add(Dense(num_labels, activation='softmax'))

#try using different optimizers and different optimizer configs
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])

print('Summary of the built model...')
print(model.summary())

La última capa del modelo es Dense(num_labels, activation =’softmax'), con num_labels=20clases, se usa ‘softmax’. La función de pérdida para loss = ‘categorical_crossentropy’, es adecuada para problemas de clasificación multiclase en aprendizaje automático.

Modelo de entrenamiento (Train Model)

num_epochs = 10
batch_size = 128
history = model.fit(x_train, y_train, 
                    batch_size = batch_size, 
                    epochs = num_epochs, 
                    verbose = 2, 
                    validation_split = 0.2)

Entrenamiento del modelo con un 20% de conjunto de validación validation_split = 20 y al usar verbose = 2, vemos la precisión de validación después de cada época. Justo después de 10 épocas, alcanzamos una precisión de validación del 90%.

Evaluación del modelo

score, acc = model.evaluate(x_test, y_test,
                       batch_size=batch_size,verbose=2)

print('Test accuracy', acc)

Test accuracy: 0.8780952383223034

Esto parece una precisión muy buena, pero ¿está realmente funcionando bien el modelo?

¿Cómo medir el rendimiento del modelo?

Consideremos que entrenamos nuestro modelo con datos desequilibrados de ejemplos anteriores de frutas y, dado que los datos están muy sesgados hacia la Clase 1 (Naranjas), el modelo se ajusta demasiado a la etiqueta de Clase 1 y la predice en la mayoría de los casos y logramos una precisión del 80%.

Lo que parece muy bueno al principio, pero mirando de cerca, es posible que nunca pueda clasificar manzanas o peras correctamente. Ahora la pregunta es si la precisión, en este caso, no es la métrica correcta para elegir, ¿qué métricas usar para medir el desempeño del modelo?

Matriz de confusión

Con clases desequilibradas, es fácil obtener una alta precisión sin realizar predicciones útiles.

Por lo tanto, la precisión como métrica de evaluación sólo tiene sentido si las etiquetas de clase están distribuidas uniformemente. En caso de clases desequilibradas, la matriz de confusión es una buena técnica para resumir el rendimiento de un algoritmo de clasificación.

 Matriz de confusión (Confusion Matrix) es una medida de rendimiento para un algoritmo de clasificación donde la salida puede ser de dos o más clases.

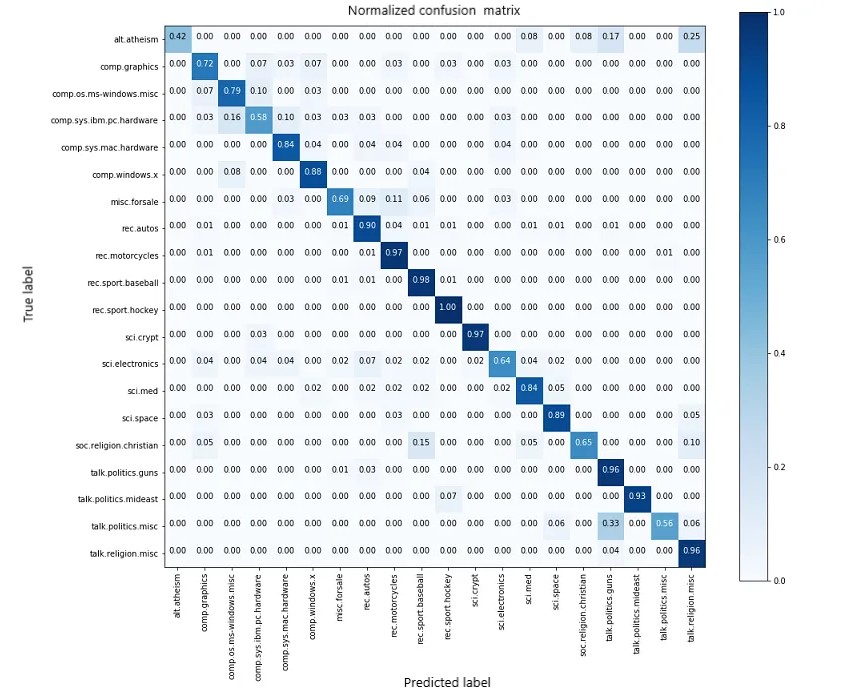
Cuando observamos de cerca la matriz de confusión, vemos que las clases [ alt.athiesm, talk.politics.misc, soc.religion.christian ] que tienen muy menos muestras [65,53, 86] respectivamente, de hecho tienen puntuaciones muy inferiores. [0,42, 0,56, 0,65] en comparación con las clases con mayor número de muestras como [ rec.sport.hockey, rec.motorcycles ].

Por lo tanto, al observar la matriz de confusión se puede ver claramente cómo se está desempeñando el modelo al clasificar varias clases.

¿Cómo mejorar el rendimiento?

Existen varias técnicas involucradas para mejorar el rendimiento de conjuntos de datos desequilibrados.

Conjunto de datos de remuestreo

Para equilibrar nuestro conjunto de datos, hay dos formas de hacerlo:

1. Submuestreo: eliminar muestras de clases sobrerrepresentadas; use esto si tiene un conjunto de datos enorme
2. Sobremuestreo: agregue más muestras de clases subrepresentadas; use esto si tiene un conjunto de datos pequeño

SMOTE (Técnica de sobremuestreo de minorías sintéticas)

SMOTE es un método de sobremuestreo. Crea muestras sintéticas de la clase minoritaria. Usamos el paquete imblearn python para sobremuestrear las clases minoritarias.

x_train.shape, y_train_shape

((4197, 15000), (4197,20))

from imblearn.over_sampling import SMOTE
#Over-sampling: SMOTE
#SMOTE (Synthetic Minority Oversampling TEchnique) consists of synthesizing elementes for the minority class,
#based on those that already exist. It works randomly picking a point from the minority class and computing
#the k-nearest neighbors for this point. The synthetic points are added between the chosen point and its neighbors.
#We'LL use ratio='minority' to resample the minority class.

smote = SMOTE('minority')

X_sm, y_sm = smote.fit_sample(x_train, y_train)
print(X_sm.shape, y_sm.shape)

((4646, 15000), (4646,20))

Tenemos 4197 muestras antes y 4646 muestras después de aplicar SMOTE, parece que SMOTE ha aumentado las muestras de clases minoritarias. Comprobaremos el rendimiento del modelo con el nuevo conjunto de datos.

history = model.fit(X_sm, y_sm,
                    batch_size = batch_size,
                    epochs = num_epochs,
                    verbose = 2,
                    class_weight = class_weight,
                    validation_split = 0.2)

Se mejoró la precisión de la validación de 90 a 94%. Probemos el modelo:

score, acc = model.evaluate(x_test, y_test,
                       batch_size=batch_size,verbose=2)

print('Test accuracy', acc)

Test accuracy: 0.8885714287984939

 

Poca mejora en la precisión de las pruebas que antes (del 87 al 88%). Echemos un vistazo ahora a la matriz de confusión:

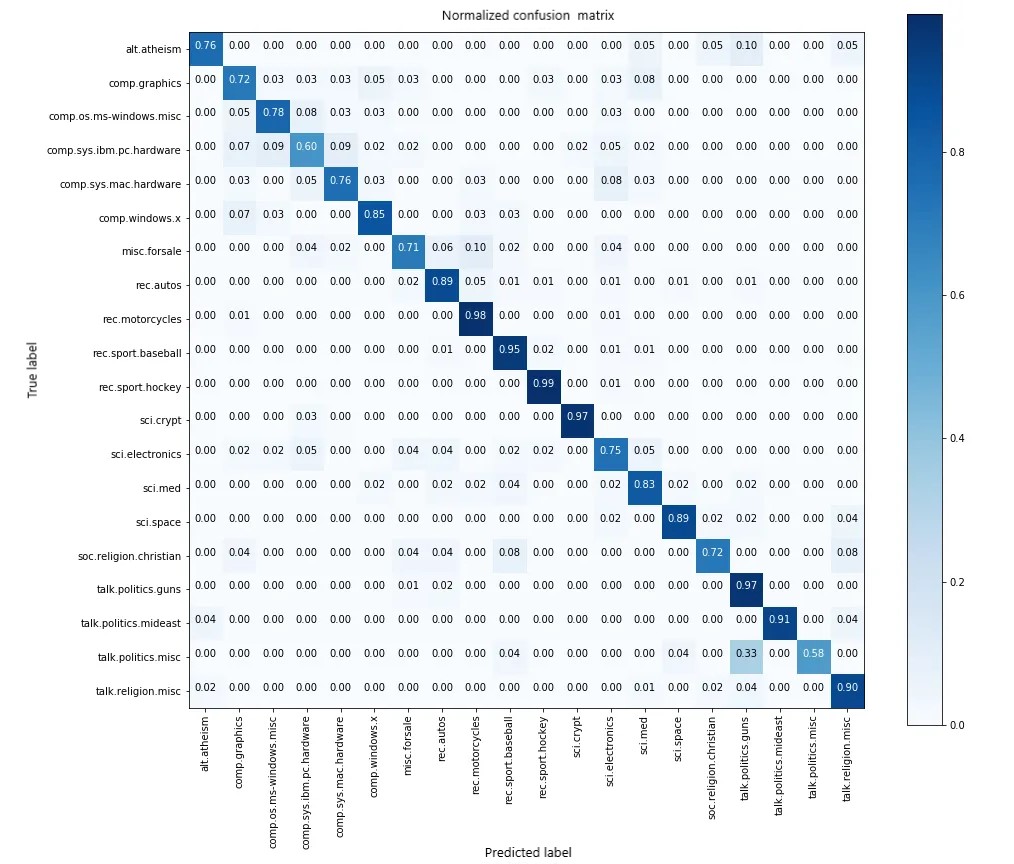
Vemos que las clases [ alt.athiesm , talk.politics.misc , sci.electronics , soc.religion.christian ] tienen puntuaciones mejoradas [0,76, 0,58, 0,75, 0,72] que antes. Por lo tanto, el modelo funciona mejor que antes, mientras que clasificar las clases aunque la precisión sea similar.

Otro truco:

Dado que las clases están desequilibradas, ¿qué tal si se proporciona algún sesgo a las clases minoritarias? Podemos estimar los pesos de las clases en scikit_learn usando compute_class_weightel parámetro ‘class_weight’mientras entrenamos el modelo.

Esto puede ayudar a proporcionar cierto sesgo hacia las clases minoritarias mientras se entrena el modelo y así ayudar a mejorar el rendimiento del modelo al clasificar varias clases.

from sklearn.utils import class_weight
class_weight = class_weight.compute_class_weight('balanced', np.unique(y_train_labels), y_train_labels)
num_epochs = 10
batch_size = 128
history = model.fit(X_sm, y_sm,
                    batch_size = batch_size,
                    epochs = num_epochs,
                    verbose = 2,
                    class_weight = class_weight,
                    validation_split = 0.2)

Curvas de recuperación de precisión

Precision-Recall es una medida útil del éxito de la predicción cuando las clases están muy desequilibradas.

Precisión es una medida de la capacidad de un modelo de clasificación para identificar sólo los puntos de datos relevantes, mientras recall es una medida de la capacidad de un modelo para encontrar todos los casos relevantes dentro de un conjunto de datos.

La curva de recuperación de precisión muestra el equilibrio entre precisión y recuperación para diferentes umbrales. Un área alta bajo la curva representa tanto un alto recuerdo como una alta precisión, donde la alta precisión se relaciona con una tasa baja de falsos positivos y la alta recuperación se relaciona con una tasa baja de falsos negativos.

Las puntuaciones altas tanto de precisión como de recuperación muestran que el clasificador arroja resultados precisos (precisión), además de devolver la mayoría de todos los resultados positivos (recuperación). Un sistema ideal con alta precisión y alta recuperación arrojará muchos resultados, con todos los resultados etiquetados correctamente.

A continuación se muestra un gráfico de recuperación de precisión para un conjunto de datos de 20 grupos de noticias utilizando scikit-learn .

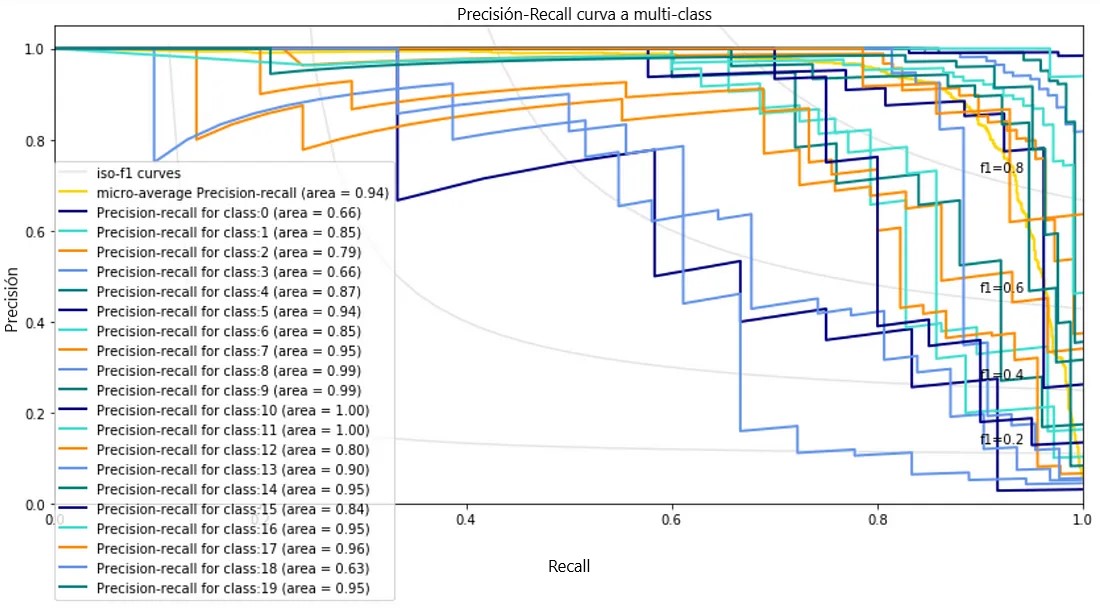
Nos gustaría que el área de la curva PR para cada clase esté cerca de 1. Excepto las clases 0, 3 y 18, el resto de las clases tienen un área superior a 0,75. Puede probar con diferentes modelos de clasificación y técnicas de ajuste de hiperparámetros para mejorar aún más el resultado.

Conclusión

Discutimos los problemas asociados con la clasificación multiclase en aprendizaje automático en un conjunto de datos desequilibrado. También demostramos cómo el uso de las herramientas y técnicas adecuadas nos ayuda a desarrollar mejores modelos de clasificación.