Tres principales enfoques de los modelos de aprendizaje automático

1. Una taxonomía de los modelos de aprendizaje automático

No existe una forma sencilla de clasificar los algoritmos de aprendizaje automático. Para un problema dado, la recopilación de todos los resultados posibles representa el espacio de muestra o el espacio de instancia .

La idea básica para crear una taxonomía de algoritmos es que dividamos el espacio de instancia utilizando una de las siguientes formas usando:

Una expresión lógica.
La geometría del espacio de instancia.
La probabilidad de clasifique el espacio de instancia.

El resultado de la transformación del espacio de instancia por un algoritmo de aprendizaje automático utilizando las técnicas anteriores debe ser exhaustivo (abarcar todos los resultados posibles) y mutuamente excluyente (no superpuesto).

2. Modelos lógicos

2.1 Modelos lógicos: modelos de árbol y modelos de reglas

Los modelos lógicos utilizan una expresión lógica para dividir el espacio de la instancia en segmentos y, por lo tanto, construir modelos de agrupación.

Una expresión lógica es una expresión que devuelve un valor booleano, es decir, un resultado Verdadero o Falso.

Una vez que los datos se agrupan utilizando una expresión lógica, los datos se dividen en agrupaciones homogéneas para el problema que estamos tratando de resolver.

Por ejemplo, para un problema de clasificación, todas las instancias del grupo pertenecen a una clase.

Existen principalmente dos tipos de modelos lógicos:

Modelos de árbol y Modelos de reglas .

Los modelos de reglas consisten en una colección de implicaciones o reglas IF-THEN.

Para los modelos basados en árboles, la “parte si” define un segmento y la “parte entonces” define el comportamiento del modelo para este segmento. Los modelos de reglas siguen el mismo razonamiento.

Los modelos de árbol pueden verse como un tipo particular de modelo de regla donde las partes si de las reglas están organizadas en una estructura de árbol.

Tanto los modelos de árbol como los modelos de reglas utilizan el mismo enfoque para el aprendizaje supervisado.

El enfoque se puede resumir en dos estrategias:

Primero podríamos encontrar el cuerpo de la regla (el concepto) que cubre un conjunto suficientemente homogéneo de ejemplos y luego encontrar una etiqueta que represente al cuerpo.
Alternativamente, podríamos enfocarlo desde la otra dirección, es decir, primero seleccionar una clase que queramos aprender y luego encontrar reglas que cubran ejemplos de la clase.

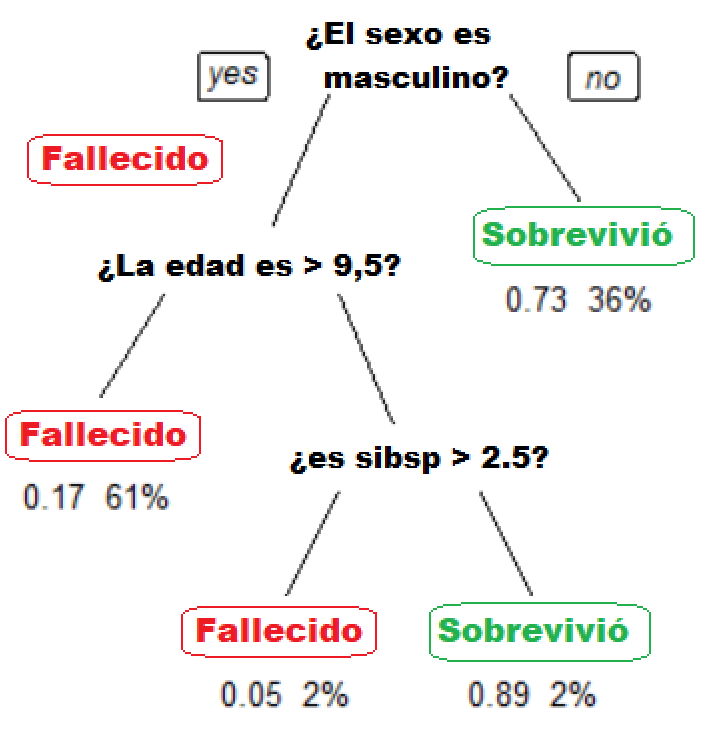
A continuación se muestra un modelo simple basado en árboles. El árbol muestra los números de supervivencia de los pasajeros en el Titanic (“sibsp” es el número de cónyuges o hermanos a bordo).

Los valores debajo de las hojas muestran la probabilidad de supervivencia y el porcentaje de observaciones en la hoja.

El modelo se puede resumir en:

Sus posibilidades de supervivencia eran altas si usted era (i) una mujer o (ii) un hombre menor de 9.5 años con menos de 2.5 hermanos.

2.2 Modelos lógicos y aprendizaje de conceptos

Para entender mejor los modelos lógicos, debemos entender la idea de concepto de aprendizaje. El aprendizaje de conceptos implica aprender expresiones lógicas o conceptos de ejemplos.

La idea de aprendizaje conceptual encaja bien con la idea de aprendizaje automático, es decir, inferir una función general a partir de ejemplos específicos de capacitación.

El aprendizaje conceptual constituye la base de los modelos basados tanto en árboles como en reglas. Más formalmente, el concepto de aprendizaje implica adquirir la definición de una categoría general de un conjunto dado de ejemplos de capacitación positivos y negativos de la categoría.

Una definición formal para el aprendizaje conceptual es

“ La deducción de una función de valor booleano a partir de ejemplos de entrenamiento de su entrada y salida”.

En el aprendizaje conceptual, solo aprendemos una descripción para la clase positiva y etiquetamos todo lo que no no satisfaga esa descripción como negativa.

El siguiente ejemplo explica esta idea con más detalle:

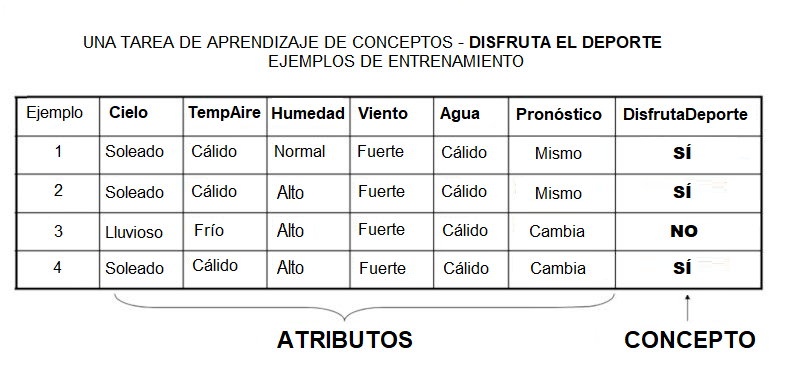
Una tarea de aprendizaje de conceptos llamada “Disfruta del deporte”, como se muestra arriba, se define mediante un conjunto de datos de algunos días de ejemplo.

Cada dato se describe mediante seis atributos. La tarea es aprender a predecir el valor de Enjoy Sport para un día arbitrario basado en los valores de sus valores de atributo. El problema puede ser representado por una serie de hipótesis.

Cada hipótesis se describe mediante una conjunción de restricciones en los atributos. Los datos de entrenamiento representan un conjunto de ejemplos positivos y negativos de la función objetivo.

En el ejemplo anterior, cada hipótesis es un vector de seis restricciones, que especifica los valores de los seis atributos: Cielo, TempAire, Humedad, Viento, Agua y Pronóstico.

La fase de entrenamiento implica aprender el conjunto de días (como una conjunción de atributos) para los que DisfrutaDeporte = SÍ.

Por lo tanto, el problema puede formularse como:

Dadas las instancias X que representan un conjunto de todos los días posibles, Cada uno descrito por los atributos:

- Cielo – (valores: Soleado, Nublado, Lluvioso),
- TempAire – (valores: Caliente, Frío),
- Humedad – (valores: Normal, Alto),
- Viento – (valores: Fuerte , Débil),
- Agua – (valores: cálido, frío),
- Pronóstico – (valores: igual, cambio).

Intente identificar una función que pueda predecir la variable objetivo Disfrute del deporte como sí / no, es decir, 1 o 0.

2.3 El aprendizaje del concepto como un problema de búsqueda y como el aprendizaje inductivo

También podemos formular el aprendizaje de conceptos como un problema de búsqueda. Podemos pensar en el aprendizaje de conceptos como una búsqueda a través de un conjunto de espacios predefinidos de posibles hipótesis para identificar una hipótesis que se ajuste mejor a los ejemplos de entrenamiento.

El aprendizaje conceptual también es un ejemplo de aprendizaje inductivo .

El aprendizaje inductivo:

También conocido como aprendizaje por descubrimiento, es un proceso en el que el alumno descubre las reglas al observar los ejemplos.
Es diferente del aprendizaje deductivo, donde los estudiantes reciben reglas que luego deben aplicar.
Se basa en la hipótesis del aprendizaje inductivo .

La hipótesis del aprendizaje inductivo postula que:

Se espera que cualquier hipótesis que se aproxime a la función objetivo sobre un conjunto suficientemente amplio de ejemplos de entrenamiento se aproxime a la función objetivo sobre otros ejemplos no observados. Esta idea es la suposición fundamental del aprendizaje inductivo.

Para resumir, en esta sección, vimos la primera clase de algoritmos en los que dividimos el espacio de instancia en función de una expresión lógica.

También discutimos cómo los modelos lógicos se basan en la teoría del aprendizaje de conceptos, que a su vez puede formularse como un aprendizaje inductivo o un problema de búsqueda.

3. Modelos geométricos

En la sección anterior, hemos visto que con los modelos lógicos, como los árboles de decisión, se usa una expresión lógica para particionar el espacio de la instancia. Dos instancias son similares cuando terminan en el mismo segmento lógico.

En esta sección, consideramos los modelos que definen la similitud considerando la geometría del espacio de instancia.

En modelos geométricos, las características podrían describirse como puntos en dos dimensiones ( x- y y -axis) o un espacio tridimensional ( x y, y z ).

Incluso cuando las características no son intrínsecamente geométricas, podrían modelarse de manera geométrica (por ejemplo, la temperatura en función del tiempo puede modelarse en dos ejes).

En los modelos geométricos, hay dos formas en que podríamos imponer similitud.

Podríamos utilizar conceptos geométricos como líneas o planos para segmentar (clasificar) el espacio de instancia. Estos se denominan Modelos lineales .
Alternativamente, podemos usar la noción geométrica de distancia para representar la similitud. En este caso, si dos puntos están juntos, tienen valores similares para las características y, por lo tanto, se pueden clasificar como similares. Llamamos modelos como Modelos basados en distancia .

3.1 Modelos lineales

Los modelos lineales son relativamente simples. En este caso, la función se representa como una combinación lineal de sus entradas.

Por lo tanto, si x ₁ y x ₂ son dos escalas o vectores de la misma dimensión y a y b ] son escalares arbitrarios, entonces ax ₁ + bx ₂ representa una combinación lineal de x _yx₂.

En el caso más simple donde f ( x ) representa una línea recta, tenemos una ecuación de la forma f ( x = ) = mx + c donde c representa la intersección y m representa la pendiente.

Los modelos lineales son paramétricos lo que significa que tienen una forma fija con un pequeño número de parámetros numéricos que deben aprenderse de los datos .

Por ejemplo, en f ( x ) = mx + c c and and c] son los parámetros que estamos tratando de aprender de los datos.

Esta técnica es diferente de los modelos de árbol o de regla, donde la estructura del modelo (por ejemplo, qué características usar en el árbol y dónde) no está prefijada de antemano .

Los modelos lineales son estable es decir, pequeñas variaciones en los datos de entrenamiento tienen solo un impacto limitado en el modelo aprendido.

En contraste, los modelos de árbol tienden a variar más con los datos de entrenamiento ya que la elección de una división diferente en la raíz del árbol generalmente significa que el resto del árbol también es diferente.

Como resultado de tener relativamente pocos parámetros, los modelos lineales tienen baja varianza y alto sesgo . Esto implica que Los modelos lineales tienen menos probabilidades de ajustar los datos de entrenamiento que otros modelos.

Sin embargo, es más probable que se adapten. Por ejemplo, si queremos aprender los límites entre países según los datos etiquetados, es probable que los modelos lineales no den una buena aproximación.

En esta sección, también podríamos usar algoritmos que incluyan métodos del kernel como la máquina de vectores de soporte (SVM).

Los métodos del kernel utilizan la función del kernel para transformar los datos en otra dimensión donde se puede lograr una separación más fácil para los datos, como el uso de un hiperplano para SVM.

3.2 Modelos basados en la distancia

Los modelos basados en la distancia son los Segunda clase de modelos geométricos. Al igual que los modelos lineales, los modelos basados en la distancia se basan en la geometría de los datos.

Como su nombre lo indica, los modelos basados en la distancia trabajan en el concepto de distancia.

En el contexto del aprendizaje automático, el concepto de distancia no se basa simplemente en la distancia física entre dos puntos. En cambio, podríamos pensar en la distancia entre dos puntos considerando el modo de transporte entre dos puntos.

Viajar entre dos ciudades en avión cubre menos distancia físicamente que en tren porque un avión no tiene restricciones. De manera similar, en el ajedrez, el concepto de distancia depende de la pieza utilizada, por ejemplo, un Obispo puede moverse en diagonal.

Por lo tanto, dependiendo de la entidad y el modo de viaje, el concepto de distancia se puede experimentar de manera diferente. Las métricas de distancia que se usan comúnmente son Euclidean, Minkowski, Manhattan, and Mahalanobis.

La distancia se aplica a través del concepto de vecinos y ejemplares . Los vecinos son puntos de proximidad con respecto a la medida de distancia expresada a través de ejemplares.

Los ejemplares son o bien centroides que encuentran un centro de masa de acuerdo con una métrica de distancia elegida o medoids que encuentran el punto de datos más central.

El centroide más utilizado es la media aritmética, que minimiza la distancia euclidiana al cuadrado de todos los demás puntos.

Notas:

El centroide representa el centro geométrico de una figura plana, es decir, la media aritmética Posición de todos los puntos en la figura desde el punto centroide. Esta definición se extiende a cualquier objeto en n espacio tridimensional: su centroide es la posición media de todos los puntos.
Los medoides son similares en concepto a los medios o centroides. Los medoides se usan más comúnmente en los datos cuando no se puede definir una media o centroide. Se utilizan en contextos donde el centroide no es representativo del conjunto de datos, como en los datos de imagen.

Los ejemplos de modelos basados en la distancia incluyen los modelos de vecino más cercano que utilizan los datos de entrenamiento como ejemplares.

Por ejemplo, en clasificación. El algoritmo K-means clustering también utiliza ejemplos para crear grupos de puntos de datos similares.

4. Modelos probabilísticos

La tercera familia de algoritmos de aprendizaje automático son los modelos probabilísticos. Hemos visto anteriormente que el algoritmo vecino más cercano k usa la idea de la distancia (por ejemplo, la distancia euclidiana) para clasificar las entidades.

Y los modelos lógicos usan una expresión lógica para dividir el espacio de la instancia. En esta sección, vemos cómo los modelos probabilísticos usan la idea de probabilidad para clasificar entidades nuevas.

Los modelos probabilísticos ven características y variables objetivo como variables aleatorias. El proceso de modelado representa y manipula el nivel de incertidumbre con respecto a estas variables.

Hay dos tipos de modelos probabilísticos:

Predictivo y Generativo . Los modelos de probabilidad predictiva utilizan la idea de una distribución de probabilidad condicional P ( Y | X Y puede predecirse a partir de X .

Los modelos generativos estiman la distribución conjunta P ( Y X ). Una vez que conocemos la distribución conjunta de los modelos generativos, podemos derivar cualquier distribución condicional o marginal que involucre las mismas variables.

Por lo tanto, el modelo generativo es capaz de crear nuevos puntos de datos y sus etiquetas, conociendo la distribución de probabilidad conjunta.

La distribución conjunta busca una relación entre dos variables. Una vez que se infiere esta relación, es posible inferir nuevos puntos de datos.

Naïve Bayes es un ejemplo de un clasificador probabilístico.

El objetivo de cualquier clasificador probabilístico tiene un conjunto de características ( x _0 hasta x _n) y un conjunto de clases ( c _0 hasta c _k, nuestro objetivo es determinar la probabilidad de las características que ocurren en cada clase, y para devolver la clase más probable.

Por lo tanto, para cada clase, debemos calcular P ( c _i | x_0, …, x_n).

Podemos hacer esto usando la regla de Bayes , definida como:

El algoritmo Naïve Bayes se basa en la idea de Probabilidad condicional. La probabilidad condicional se basa en encontrar la probabilidad de que algo suceda, dado que otra cosa ya ha sucedido.

La tarea del algoritmo es mirar la evidencia y determinar la probabilidad de una clase específica y asignar una etiqueta de acuerdo a cada entidad.

Conclusión

La discusión anterior presenta una forma de clasificar los algoritmos en función de sus fundamentos matemáticos. Si bien la discusión se simplifica, proporciona una forma integral de explorar algoritmos desde los primeros principios.