Marco práctico
Este tutorial es una continuación de mi publicación anterior de árboles de decisión. Si conoce los conceptos básicos del algoritmo de aprendizaje basado en el árbol y, más específicamente, el algoritmo de árboles de decisión en Machine Learning. Puede continuar su búsqueda para dominar el “algoritmo de árboles de decisión”.
Pero si usted es un principiante o un novato o no puede recordar el concepto, le sugiero que pase por Parte I de esta publicación porque la ganancia de información de Parte I es mayor que Parte II (si no obtuvo esto – >> Parte I << -). Esta publicación podría ser larga, pero vale la pena adquirir conocimiento.
Introducción
Esta publicación está dirigida al lado práctico de los árboles de decisión en Machine Learning en lugar de a la teoría detrás de él.
Según las fuentes,
Hasta 60,000 veces mejor parece. En general, es más fácil comprender las imágenes que leer bloques enteros de texto. De hecho, un enorme 90% de la información que recibe el cerebro es no verbal.
Y, por supuesto, el primer lenguaje escrito de los humanos consistía en imágenes. Nuestro cerebro está programado para comprender las imágenes mejor que el texto.
Debido a esto, las personas recuerdan hasta el 80% de lo que ven en comparación con solo alrededor del 20% de lo que leen. Entonces, cuando se trata de memorabilidad, los elementos visuales son clave para la creación de contenido.
Por lo tanto, en esta publicación, entenderemos los árboles de decisión en Machine Learning y como funciona el árbol de decisión (representación gráfica) en lugar de la explicación textual monótona.
Luego, utilizaremos el Algoritmo del árbol de decisión en un conjunto de datos para familiarizarnos con la solución del problema con el algoritmo (en Python) y visualizar el árbol que creó.
Después de eso, tengo un contenido adicional que está ligeramente sesgado hacia la parte avanzada, pero obtener una comprensión al respecto te hará sentir curiosidad por aprender más y te dejarás llevar por el proceso de aprendizaje.
Entonces, ¿Qué sabemos hasta ahora?
Los árboles de decisión en Machine Learning se pueden usar para predecir la característica objetivo de una instancia de consulta desconocida mediante la construcción de un modelo basado en datos existentes para los que se conocen los valores de la característica objetivo (aprendizaje supervisado).
Además, sabemos que este modelo puede hacer predicciones para instancias de consulta desconocidas porque modela la relación entre las características descriptivas conocidas y la característica de destino conocido.
En nuestro siguiente ejemplo, el modelo de árbol aprende “cómo se ve una especie animal específica”, respectivamente, la combinación de valores de características descriptivas distintivas para especies animales.
Además, sabemos que para entrenar un modelo de árboles de decisión en Machine Learning necesitamos un conjunto de datos que consta de varios ejemplos de entrenamiento caracterizados por varias características descriptivas y una característica objetivo.
Ejemplo de trabajo del algoritmo de árboles de decisión en Machine Learning
Queremos, dado un conjunto de datos, entrenar un modelo que aprenda la relación entre las características descriptivas y un objetivo característica de tal manera que podamos presentar al modelo un conjunto nuevo e invisible de instancias de consulta y predecir los valores de la característica de destino para estas instancias de consulta .
Recapitulemos más la forma general de un árbol de decisión. Sabemos que tenemos en la parte inferior de los nodos de la hoja del árbol que contienen (en el caso óptimo) valores de características de destino.
Para hacer esto más ilustrativo, usamos como ejemplo práctico una versión simplificada del conjunto de datos de Clasificación de Animales del Zoológico de aprendizaje automático de UCI que incluye propiedades de animales como características descriptivas y la y la especie animal como característica objetivo .
En nuestro ejemplo, los animales se clasifican como mamíferos o reptiles en función de si tienen dientes, tienen patas y respiran. El conjunto de datos tiene el siguiente aspecto:
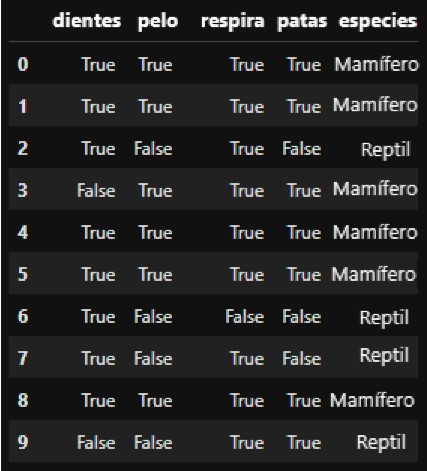
Por lo tanto, para volver a nuestra pregunta inicial, cada nodo de hoja debería (en el mejor de los casos) solo contener “Mamíferos” o “Reptiles”. La tarea para nosotros ahora es encontrar la mejor “forma” de dividir el conjunto de datos para que esto se pueda lograr.
¿Qué quiero decir cuando digo dividir ?
Considere bien el conjunto de datos anterior y piense en lo que debe hacerse para dividir el conjunto de datos en un Conjunto de datos 1 que contiene como valores de características objetivo (especies) solo Mamíferos y un Conjunto de datos 2, que contiene solo Reptiles.
Para lograr eso, en este ejemplo simplificado, solo necesitamos la característica descriptiva cabello ya que si el cabello es VERDADERO, la especie asociada es siempre un Mamífero. Por lo tanto, en este caso, nuestro modelo de árbol se vería así:

Es decir, hemos dividido nuestro conjunto de datos haciendo la pregunta de si el animal tiene pelo o no. Ahora, en ese caso, la división ha sido muy fácil para nosotros, porque podríamos identificar fácilmente la relación de clasificación entre tener pelo y ser mamífero y viceversa.
Algunos pueden diferenciar fácilmente este conjunto de datos de la tabla porque sabían que los mamíferos tienen pelo y los reptiles no. Pero una máquina puede detectarlo tan fácilmente.
Además, la mayoría de las veces los conjuntos de datos no son tan fácilmente separables y debemos dividir el conjunto de datos más de una vez (“hacer más de una pregunta”).
Por lo tanto, dejar el cabello sin otro atributo hace que sea fácil obtener nodos de hoja directamente. Omitiremos el atributo del cabello para obtener una situación similar a la del mundo real.

Por lo tanto, la entropía de nuestro conjunto de datos con respecto a la característica objetivo se calcula con:
- Entropía del nodo primario = – (6/10) ∗ log2 ( 6/10) – (4/10) ∗ log2 (4/10) = 0.971
- Entropía de (dientes == Verdadero) = – (5/8) log2 (5/8) – (3/8) log2 (3/8) = 0.95
- Entropía de (dientes == Falso) = – (1/2) log2 (1/2) – (1/2) log2 (1/2) = 1
- Entropía para división en dientes = 8/10 (0.95) + 2/10 (1) = 0.96
- Ganancia de información – InfoGain = 0.971- 0.96 = 0.011
Denotaremos entropía por “H ()”:
- Respira: H(respira) = (9/10 ∗ – ((6/9 ∗ log2 (6/9)) + (3/9 ∗ log2 (3/9))) + 1/10 ∗ – ((0) + (1 ∗ log2 (1)))) = 0.82647
- Ganancia de información – InfoGain (respira) = 0.971−0.82647 = 0.1445
- Piernas: H(piernas) = 7/10 ∗ – ((6/7 ∗ log2 ( 6 6 / 7)) + (1/7 ∗ log2 (1/7))) + 3/10 ∗ – ((0) + (1 ∗ log2 (1))) = 0.41417
- Ganancia de información – InfoGain (piernas) = 0.971−0.41417 = 0.5568
Por lo tanto, la división del conjunto de datos a lo largo de la función piernas da como resultado la mayor ganancia de información y deberíamos usar esta función para nuestro nodo raíz.
Por lo tanto, por el momento, el modelo de árboles de decisión en Machine Learning se ve así:
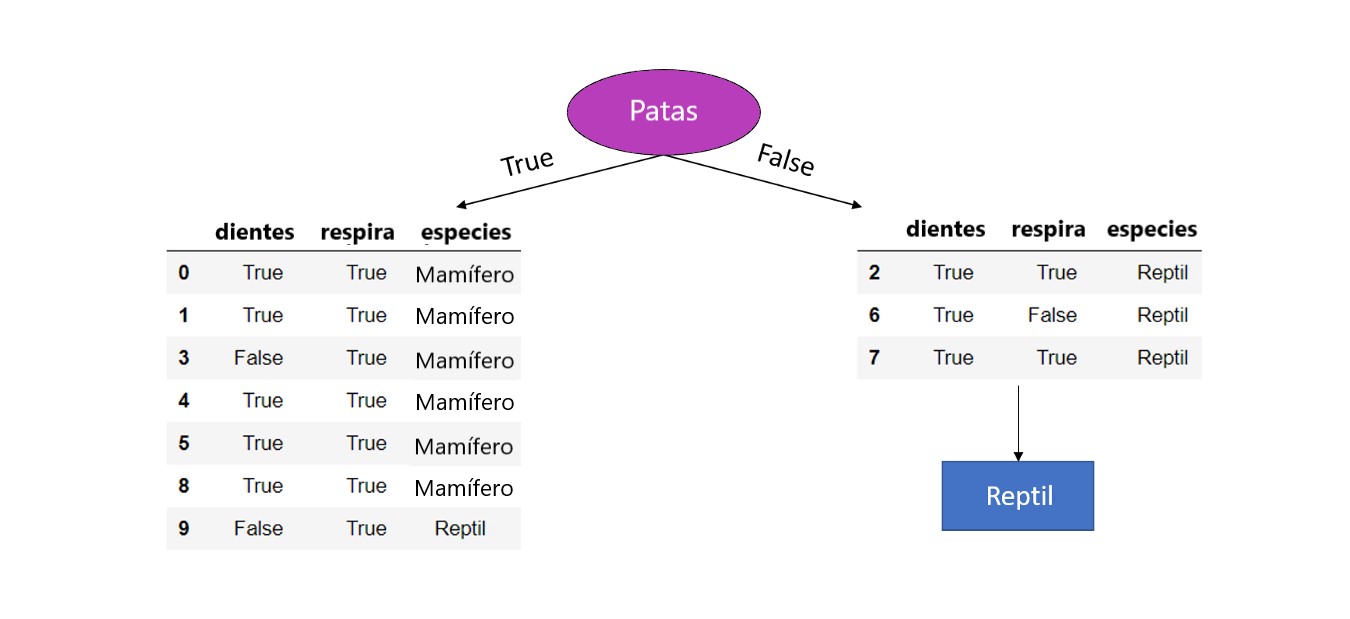
Vemos que para las piernas == Falso, los valores de la característica objetivo del conjunto de datos restante son todos Reptil y, por lo tanto, configuramos esto como nodo hoja porque tenemos un conjunto de datos puro (dividir aún más el conjunto de datos en cualquiera de las dos características restantes no conduciría a un resultado diferente o más preciso ya que, haga lo que hagamos después de este punto, la predicción seguirá siendo Reptil ) .
Además, verá que la característica piernas ya no se incluye en los conjuntos de datos restantes. Debido a que ya hemos usado esta característica (categórica) para dividir el conjunto de datos, no se debe usar más.
Hasta ahora, hemos encontrado la característica para el nodo raíz y un nodo hoja para piernas == Falso . Ahora se deben realizar los mismos pasos para el cálculo de la ganancia de información también para el conjunto de datos restante para piernas == Verdadero ya que aquí todavía tenemos una mezcla de diferentes valores de características objetivo. Por lo tanto:
Cálculo de ganancia de información para las características dentadas y respira para el conjunto de datos restante piernas == Verdadero.
La entropía del (nuevo) conjunto de datos secundario después de la primera división:
H (D) = – ((67 ∗ log2 (67)) + (17 ∗ log2 (17))) = 0.5917
- Dientes: H (dientes) = 5/7 ∗ – ((1 ∗ log2 (1)) + (0)) + 2/7 ∗ – ((1/2 ∗ log2 (1/2)) + (1/2 ∗ log2 (1/2))) = 0.285
- Ganancia de información – InfoGain (dientes) = 0.5917−0.285 = 0.3067
- Respira: H (respira)= 77 ∗ – ((67 ∗ log2 (67)) + (17 ∗ log2 (17))) + 0 = 5917
- Ganancia de información – InfoGain (dientes) = 0.5917−0.5917 = 0
El conjunto de datos para dientes == False todavía contiene una mezcla de valores de características de destino diferentes por las cuales procedemos a particionar el último característica izquierda (== respira)
De ahí el el árbol completamente crecido se ve así:
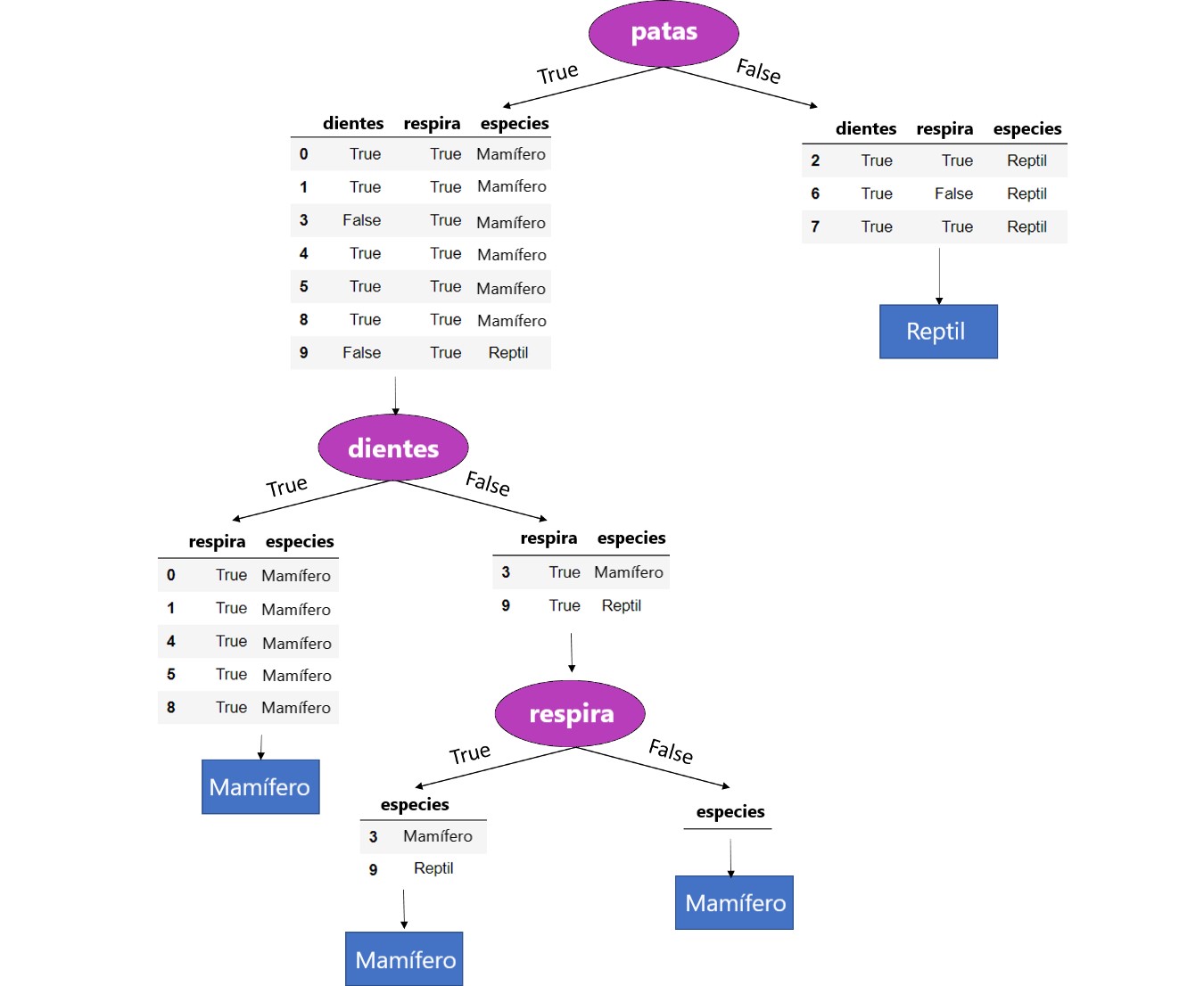
Tenga en cuenta la última división (nodo) donde el conjunto de datos se dividió en la característica respira . Aquí la función de respiraciones solo contiene datos donde respiraciones == Verdadero.
Por lo tanto, para respiraciones == Falso no hay instancias en el conjunto de datos y, por lo tanto, no hay un subconjunto de datos que se pueda construir. En ese caso, devolvemos el valor de característica objetivo más frecuente en el conjunto de datos original que es Mamífero . Este es un ejemplo de cómo nuestro modelo de árbol se generaliza detrás de los datos de entrenamiento.
Si consideramos la otra rama, es decir respira == Verdadero sabemos que después de dividir el conjunto de datos en los valores de un característica específica (respira {True, False}) en nuestro caso, la característica debe ser eliminada.
Bueno, eso lleva a un conjunto de datos donde no hay más funciones disponibles para dividir aún más el conjunto de datos. Por lo tanto, dejamos de hacer crecer el árbol y devolvemos el valor de modo del nodo primario directo que es “Mamífero”.
Construcción clasificador árboles de decisión en Machine Learning en Scikit-learn
Importando las bibliotecas requeridas
Primero carguemos las bibliotecas requeridas:
# Load libraries import pandas as pd from sklearn.tree import DecisionTreeClassifier # Import Decision Tree Classifier from sklearn.model_selection import train_test_split # Import train_test_split function from sklearn import metrics #Import scikit-learn metrics module for accuracy calculation
Cargando datos
Primero carguemos el conjunto de datos de Pima Indian Diabetes requerido usando la función de lectura CSV de pandas. Puede descargar los datos aquí.
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
# load dataset
pima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)
pima.head()
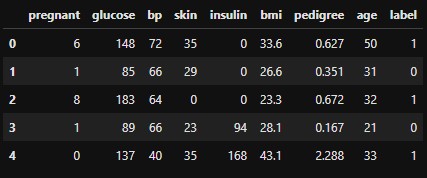
Selección de características
Aquí, debe dividir las columnas dadas en dos tipos de variables dependientes (o variables objetivo) y variables independientes (o variables de características).
#split dataset in features and target variable feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree'] X = pima[feature_cols] # Features y = pima.label # Target variable
División de datos
Para comprender el rendimiento del modelo, dividiendo el conjunto de datos en un conjunto de entrenamiento y un conjunto de prueba es una buena estrategia.
Dividamos el conjunto de datos usando la función train_test_split (). Debe pasar 3 características de parámetros, objetivo y tamaño de conjunto de prueba.
# Split dataset into training set and test set X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1) # 70% training and 30% test
Creación del modelo de árbol de decisión
Creemos un modelo de árbol de decisión utilizando Scikit-learn. Conozca sklearn sklearn.tree.DecisionTreeClassifier¶
# Create Decision Tree classifer object clf = DecisionTreeClassifier()
# Train Decision Tree Classifer clf = clf.fit(X_train,y_train)
#Predict the response for test dataset y_pred = clf.predict(X_test)
Modelo de evaluación
Vamos a estimar, con qué precisión el clasificador o modelo puede predecir el tipo de cultivares.La precisión se puede calcular comparando los valores reales del conjunto de pruebas y los valores pronosticados.
# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
Accuracy: 0.6753246753246753
Bueno, obtuvo una tasa de clasificación del 67.53%, considerada como una buena precisión. Puede mejorar esta precisión ajustando los parámetros en el Algoritmo del árbol de decisión.
Visualizando los árboles de decisión en Machine Learning
Puede usar la función export_graphviz de Scikit-learn para mostrar el árbol dentro de un cuaderno Jupyter. Para trazar el árbol, también necesita instalar Graphviz y pydotplus.
pip install graphviz pip install pydotplus
La función export_graphviz convierte el clasificador del árbol de decisión en un archivo de puntos y pydotplus convierte este archivo de puntos a png o formulario visualizable en Jupyter.
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplusdot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('diabetes.png')
Image(graph.create_png())

En el diagrama del árbol de decisiones, cada nodo interno tiene una regla de decisión que divide los datos. Gini se conoce como relación de Gini, que mide la impureza del nodo. Puede decir que un nodo es puro cuando todos sus registros pertenecen a la misma clase, tales nodos conocidos como nodo hoja.
Aquí, el árbol resultante no se poda. Este árbol sin podar es inexplicable y no es fácil de entender. En la siguiente sección, optimicémosla podando.
Optimizando el rendimiento del árbol de decisión
Como puede ver arriba, el árbol es demasiado vasto y no tan preciso. Este árbol también lleva tiempo, por lo que para obtener mejores resultados, necesitamos optimizar el árbol ajustando el parámetro.
Aquí explicaré solo el parámetro importante del Algoritmo del árbol de decisión, su ajuste requerirá una publicación de blog completamente nueva. Si observa los parámetros que puede tomar el DecisionTreeClassifier se sorprenderá, echemos un vistazo a algunos de ellos.
criterio: Este parámetro determina cómo la impureza de Se medirá una división. El valor predeterminado es “gini”, pero también puede usar “entropía” como medida de impureza.
divisor: Así es como el árbol de decisión busca las características para una división. El valor predeterminado se establece en “mejor”. Es decir, para cada nodo, el algoritmo considera todas las características y elige la mejor división.
Si decide establecer el parámetro del divisor en “aleatorio”, se considerará un subconjunto aleatorio de características. La división se realizará por la mejor característica dentro del subconjunto aleatorio.
El tamaño del subconjunto aleatorio está determinado por el parámetro max_features. Aquí es en parte donde un bosque aleatorio recibe su nombre.
max_depth: Esto determina la profundidad máxima del árbol. En nuestro caso, usamos una profundidad de dos para hacer nuestro árbol de decisión. El valor predeterminado se establece en none.
Esto a menudo dará como resultado árboles de decisión sobreajustados. El parámetro de profundidad es una de las formas en que podemos regularizar el árbol, o limitar la forma en que crece para evitar sobreajuste .
min_samples_split: El número mínimo de muestras un nodo debe contener para considerar la división. El valor predeterminado es dos. Puede usar este parámetro para regularizar su árbol.
min_samples_leaf: El número mínimo de muestras necesarias para ser considerado un nodo hoja. El valor predeterminado se establece en uno. Use este parámetro para limitar el crecimiento del árbol.
max_features: El número de características a considerar al buscar la mejor división. Si no se establece este valor, el árbol de decisión considerará todas las características disponibles para hacer la mejor división. Dependiendo de su aplicación, a menudo es una buena idea ajustar este parámetro.
Para fines de sintaxis, establezcamos algunos de estos parámetros:
Setting parameterstree = DecisionTreeClassifier(criterion = "entropy", splitter = "random", max_depth = 2, min_samples_split = 5,min_samples_leaf = 2, max_features = 2).fit(X,y)
Avanzado: Overfitting y Underfitting
En la práctica, no es raro que un árbol tenga 10 divisiones entre la parte superior- nivel (todos los datos) y una hoja. A medida que el árbol se hace más profundo, el conjunto de datos se divide en hojas con menos datos.
Si un árbol solo tenía 1 división, divide los datos en 2 grupos. Si cada grupo se divide nuevamente, obtendríamos 4 grupos de datos. Dividir cada uno de esos nuevamente crearía 8 grupos.
Si seguimos duplicando el número de grupos agregando más divisiones en cada nivel, tendremos 210210 grupos de datos para cuando lleguemos al décimo nivel. Son 1024 hojas.
Cuando dividimos los datos entre muchas hojas, también tenemos menos datos en cada hoja. Las hojas con muy pocos datos harán predicciones muy cercanas a los valores reales de esos hogares, pero pueden hacer predicciones muy poco confiables para nuevos datos (porque cada predicción se basa en unos pocos datos).
Este es un fenómeno llamado sobreajuste donde un modelo coincide con los datos de entrenamiento casi a la perfección pero tiene una pobre validación y otros datos nuevos. Por otro lado, si hacemos que nuestro árbol sea muy poco profundo, no divide los datos en grupos muy distintos.
En el extremo, si un árbol divide los datos en solo 2 o 4, cada grupo aún tiene un amplio variedad de datos. Las predicciones resultantes pueden estar muy lejos para la mayoría de los datos, incluso en los datos de entrenamiento (y también será malo en la validación por la misma razón).
Cuando un modelo no logra capturar distinciones y patrones importantes en los datos, por lo que funciona mal incluso en los datos de entrenamiento, eso se denomina falta de ajuste .
Dado que nos preocupamos por la precisión de los nuevos datos, que estimamos a partir de nuestros datos de validación, queremos encontrar el punto óptimo entre la adaptación insuficiente y la adaptación excesiva.
Visualmente, queremos el punto bajo de la curva de validación (roja) en la imagen que se muestra a continuación:
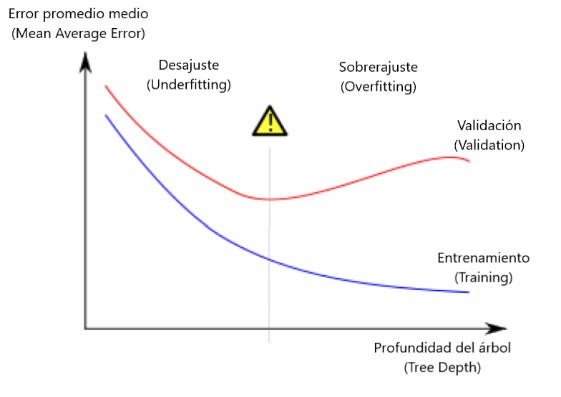
Eso es todo amigos. ¡¡¡Feliz aprendizaje!!! 🙂