TensorFlow: Comenzando en Google Colaboratory

Apertura de un cuaderno Colab

Cuando use Colab por primera vez, puede lanzar un nuevo cuaderno aquí:

Una vez que haya creado una libreta, se guardará en su Google Drive (carpeta Colab Notebooks). Puede acceder a él visitando su página de Google Drive, luego haga doble clic en el nombre del archivo o haga clic con el botón derecho y luego elija “Abrir con Colab“.

Conectando con GitHub

Los constructores de Colab son tan atentos que incluso incorporan la funcionalidad de comprometerse con Github.

Para conectarse con GitHub, primero debe crear un repositorio con una rama maestra en GitHub. Luego, en el menú desplegable, seleccione “Archivo: guardar una copia en GitHub”. Se le pedirá que autorice solo por primera vez. Lo que es útil es que incluso le permite incluir un botón “Abrir en Colab” en su cuaderno de esta manera:

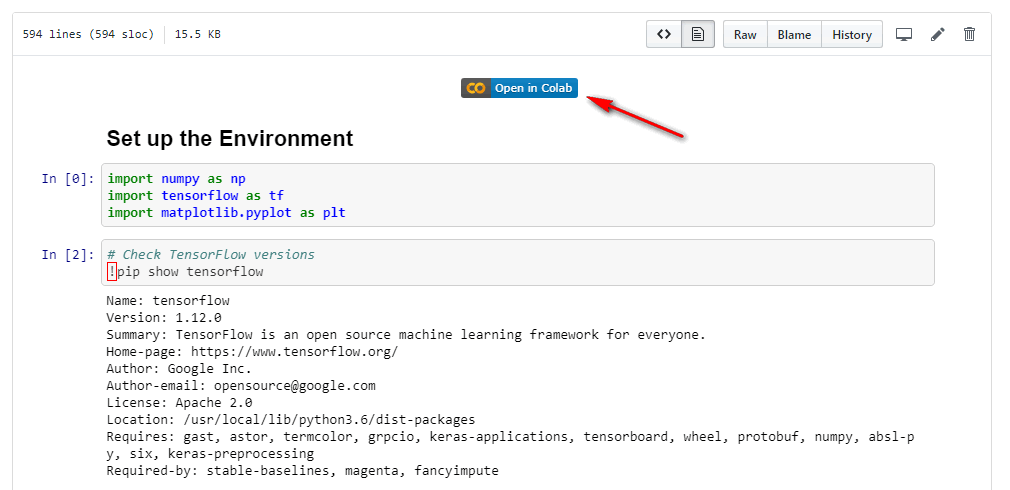
Habilitar el soporte de GPU

Para activar la GPU para sus proyectos de aprendizaje profundo, solo vaya al menú desplegable y seleccione “Tiempo de ejecución – Cambiar tipo de tiempo de ejecución – Acelerador de hardware” y elija GPU.

Trabajando con celulas

En su mayor parte, es exactamente lo mismo con un portátil Jupyter local. Por ejemplo, para ejecutar una celda de código, puede simplemente presionar “Shift + Enter”. Echa un vistazo a los métodos abreviados de teclado que se usan a continuación (en Windows con Chrome):

• Ejecutar celda: “Shift + Enter”
• Eliminar celda: “Ctrl + M, luego D”
• Deshacer: “Ctrl + Shift + Z”
• Convertir a celda de código: “Ctrl + M, luego Y”
• Convertir a celda de reducción: “Ctrl + M, luego M”
• Guardar cuaderno: “Ctrl + S”
• Abre la pantalla de acceso directo: “Ctrl + M, luego H”

 

Tensorflow: Tensores

TensorFlow basa su nombre en la palabra “tensor”. ¿Qué es un tensor de todos modos? En definitiva, una matriz multidimensional. ¡A ver qué significa eso!

Tenemos:

• Un solo número, por ejemplo, 6, lo llamamos ” escalar “;
• Tres números, por ejemplo, [6, 8, 9], llamamos a eso un ” vector“;
• Una tabla de números, por ejemplo [[6, 8, 9], [2, 5, 7]], lo llamamos una ” matriz ” (que tiene dos filas y tres columnas);
• Una tabla de tabla de números , por ejemplo [[[6, 8, 9], [2, 5, 7]], [[6, 8, 9], [2, 5, 7]]], y … Nos estamos quedando sin palabras 🙁 ¡Mi amigo, que es un tensor ! Un tensor es solo una forma generalizada de matrices que puede tener cualquier número de dimensiones .

En las jergas TensorFlow, un escalar es un tensor de rango 0, un vector es rango 1 y rango de matriz 2, etc. Hay tres tipos de tensores de uso frecuente: constante, variable y marcador de posición, que se explican a continuación.

Tensorflow: Tipos de tensores

Las constantes son exactamente a lo que se refieren sus nombres. Son los números fijos en tu ecuación. Para definir una constante, podemos hacer esto:

a = tf.constant (1, name = 'a_var') 
b = tf.constant (2, name = 'b_bar')

Aparte del valor 1, también podemos proporcionar un nombre como “a_var” para el tensor que está separado del nombre de la variable de Python “a”. Es opcional, pero será útil en operaciones posteriores y en la resolución de problemas.

Después de definir, si imprimimos la variable a, tendremos:

<tf.Tensor 'a_var: 0' shape = () dtype = int32>

Las variables son los parámetros del modelo a optimizar, por ejemplo, los pesos y sesgos en sus redes neuronales. Del mismo modo, también podemos definir una variable y mostrar sus contenidos de esta manera:

c = tf.Variable (a + b) 
c

y tiene esta salida:

<tf.Variable 'Variable: 0' shape = () dtype = int32_ref>

Pero es importante tener en cuenta que todas las variables deben inicializarse antes de usarse de esta manera:

init = tf.global_variables_initializer ()

Es posible que haya notado que los valores de a y b, es decir, los enteros 1 y 2 no se muestran en ninguna parte, ¿por qué?

Esa es una característica importante de TensorFlow: “ejecución lenta”, lo que significa que las cosas se definen primero, pero no se ejecutan. Solo se ejecuta cuando le decimos que lo haga, lo cual se hace a través de la ejecución de una sesión. (Tenga en cuenta que TensorFlow también tiene una ejecución impecable. Consulte aquí para obtener más información)

Sesion y grafica computacional

Ahora definamos una sesión y la ejecutamos:

con tf.Session () como session:                     
    session.run (init)                             
    print (session.run (c))

Observe que dentro de la sesión ejecutamos tanto la inicialización de variables como el cálculo de c. Definimos c como la suma de a y b:

c = tf.Variable (a + b)

Esto, en términos de TensorFlow y Deep Learning, es el “gráfico computacional”. Suena bastante sofisticado, ¿verdad? ¡Pero en realidad es solo una expresión del cálculo que queremos realizar!

Marcador de posición

Otro tipo de tensor importante es el marcador de posición . Su caso de uso es mantener el lugar donde se suministrarán los datos. Por ejemplo, definimos un gráfico computacional, y tenemos muchos datos de capacitación, luego podemos usar marcadores de posición para indicar que los introduciremos más adelante.

Veamos un ejemplo. Digamos que tenemos una ecuación como esta:

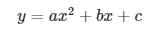
En lugar de una sola entrada x, tenemos un vector de x. Entonces podemos usar un marcador de posición para definir x:

x = tf.placeholder (dtype = tf.float32)

También necesitamos los coeficientes. Usemos constantes:

a = tf.constant (1, dtype = tf.float32) 
b = tf.constant (-20, dtype = tf.float32) 
c = tf.constant (-100, dtype = tf.float32)

Ahora hagamos el gráfico computacional y proporcionemos los valores de entrada para x:

y = a * (x ** 2) + b * x + c 
x_feed = np.linspace (-10, 30, num = 10)

Y finalmente, podemos ejecutarlo:

con tf.Session () como sess: 
  results = sess.run (y, feed_dict = {x: x_feed}) 
imprimir (resultados)

lo que nos da:

[200. 41.975304 -76.54321 -155.55554 -195.06174 -195.06174 -155.55554 -76.54324 41.97534 200.]

TensorFlow: Poniendolo todo junto

Ahora que tenemos los conceptos básicos de TensorFlow, hagamos un mini proyecto para construir un modelo de regresión lineal, también conocido como una red neuronal 🙂 (El código está adaptado del ejemplo dado en la guía de TensorFlow aquí )

Digamos que tenemos un montón de pares de valores x, y, y necesitamos encontrar la mejor línea de ajuste. Primero, dado que tanto x como y tienen valores para ser alimentados en el modelo, los definiremos como marcadores de posición:

x = tf.placeholder (dtype = tf.float32, shape = (Ninguno, 1)) 
y_true = tf.placeholder (dtype = tf.float32, shape = (None, 1))

El número de filas se define como Ninguno para tener la flexibilidad de alimentar cualquier número de filas que queramos.

A continuación, necesitamos definir un modelo. En este caso aquí, nuestro modelo tiene solo una capa con un peso y un sesgo.

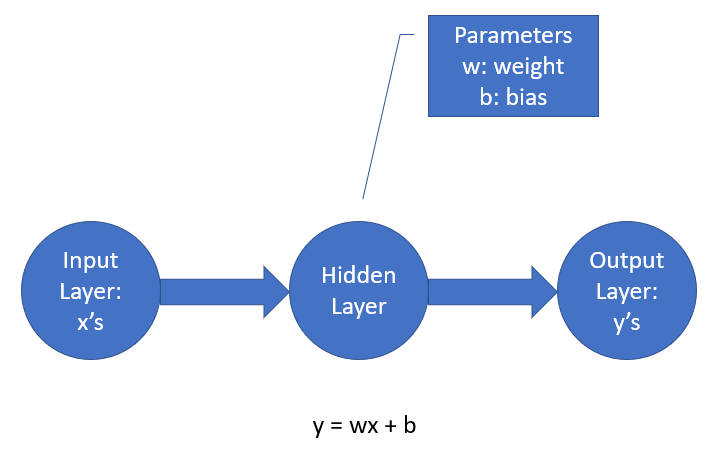
TensorFlow nos permite definir capas de redes neuronales muy fácilmente:

linear_model = tf.layers.Dense ( 
                   unidades = 1, 
                   bias_initializer = tf.constant_initializer (1)) 
y_pred = linear_model (x)

El número de unidades se establece en uno ya que solo tenemos un nodo en la capa oculta.

Además, necesitamos tener una función de pérdida y configurar el método de optimización. La función de pérdida es básicamente una forma de medir qué tan malo es nuestro modelo cuando se mide utilizando los datos de entrenamiento, por lo que, por supuesto, queremos que se minimice. Usaremos el algoritmo de descenso de gradiente para optimizar esta función de pérdida (explicaré el descenso de gradiente en una publicación futura).

optimizador = tf.train.GradientDescentOptimizer (0.01) 
train = optimizer.minimize (pérdida)

Luego podemos inicializar todas las variables. En este caso aquí, todas nuestras variables, incluido el peso y el sesgo, forman parte de la capa que definimos anteriormente.

init = tf.global_variables_initializer ()

Por último, podemos proporcionar los datos de capacitación para los marcadores de posición y comenzar la capacitación:

x_values ​​= np.array ([[1], [2], [3], [4]]) 
y_values ​​= np.array ([[0], [-1], [-2], [-3]] )

con tf.Session () como sess: 
  sess.run (init) 
  para i en el rango (1000): 
    _, loss_value = sess.run ((train, loss), 
                             feed_dict = {x: x_values, y_true: y_values})

y podemos obtener los pesos y hacer las predicciones así:

pesos = sess.run (linear_model.weights) 
bias = sess.run (linear_model.bias) 
preds = sess.run (y_pred, 
                 feed_dict = {x: x_values})

lo que da lugar a estas predicciones:

[[-0.00847495] [-1.0041066] [-1.9997383] [-2.99537]]

Si tiene curiosidad como yo, puede verificar que el modelo hizo las predicciones usando su peso y sesgo entrenados por:

w = pesos [0] .tolist () [0] [0] 
b = pesos [1] .tolist () [0] 
x_values ​​* w + b

Lo que nos da exactamente el mismo resultado!

matriz ([[- 0.00847495], [-1.00410664], [-1.99973834], [-2.99537003]])