Selección de Machine Learning métricas de regresión (MSE) – Parte 2.
En este artículo Parte 2, discutiré la utilidad de cada métrica de regresión según el objetivo y el problema que intentemos resolver. La Parte 1 presentó los primeros cuatro indicadores como se muestra a continuación, mientras que los restantes se presentan en este artículo. Recordemos primero las principales Machine Learning metricas de regresión:
- (MSE) – Error cuadrático medio
- (RMSE) – Error cuadrático medio
- (MAE) – Error absoluto medio
- (R²) – R al cuadrado (R²)
- R cuadrado ajustado (R²)
- (MSPE) Error de porcentaje cuadrático medio
- (MAPE)Error porcentual absoluto medio
- (RMSLE) – Error logarítmico cuadrático medio
R cuadrado ajustado (R²)
R² muestra qué tan bien los términos (puntos de datos) se ajustan a una curva o línea. El R2 ajustado también indica qué tan bien se ajustan los términos a una curva o línea, pero se ajusta para el número de términos en un modelo. Si agrega más y más variables inútiles a un modelo, la R cuadrada ajustada disminuirá. Si agrega más variables útiles , aumentará R cuadrado ajustado. R² ajustado siempre será menor o igual a R².

donde n es el número total de observaciones y k es el número de regresores independientes, es decir, el número de variables en su modelo, excluyendo la constante.
Machine Learning de métricas de regresión: Diferencia principal entre R² ajustado y R²
Tanto R² como el R² ajustado le dan una idea de cuántos puntos de datos caen dentro de la línea de la ecuación de regresión . Sin embargo, R² supone que cada variable única explica la variación en la variable dependiente .
El R² ajustado le indica el porcentaje de variación explicado solo por las variables independientes que realmente afectan la variable dependiente.
En realidad, el R² ajustado lo penalizará por agregar variables independientes (K en la ecuación) que no se ajusten al modelo.
¿Por qué?
En el análisis de regresión , puede ser tentador agregar más variables a los datos a medida que los piensa. Algunas de esas variables serán significativas, pero no puede estar seguro de que la importancia sea por casualidad.
El R² ajustado compensará esto al penalizarte por esas variables adicionales.
Problemas con R² que se corrigen con un R² ajustado
- R² aumenta con cada predictor agregado a un modelo. Como R² siempre aumenta y nunca disminuye, puede parecer que se ajusta mejor con los términos que agregue al modelo. Esto puede ser completamente engañoso.
- De manera similar, si su modelo tiene demasiados términos y demasiados polinomios de alto orden, puede encontrar el problema de sobre-ajustar los datos. Cuando se ajustan en exceso los datos, un valor de R² engañosamente alto puede llevar a proyecciones engañosas.
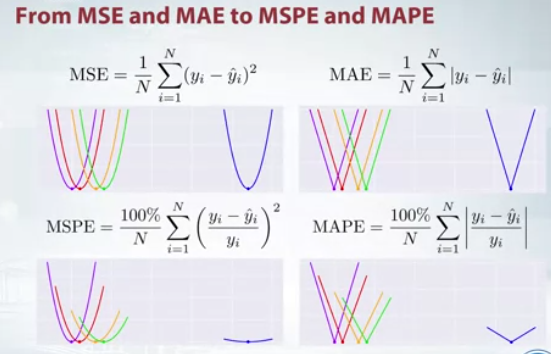
Todas las metricas que hemos examinado hasta este punto suponen que cada predicción proporciona información igualmente precisa sobre la variación del error. MSPE y MAPE no siguen esta suposición.
Error de porcentaje cuadrático medio (MSPE)
Pensemos en el siguiente problema. Nuestro objetivo es predecir, ¿Cuántas computadoras portátiles venderán dos tiendas?
- Tienda 1: predice 9, se vende 10, MSE = 1
- Tienda 2: predijo 999, se vendió 1000, MSE = 1
O incluso,
- Tienda 1: predice 9, se vende 10, MSE = 1
- Tienda 2: predicho 900, vendido 1000, MSE = 10000
MSE es el mismo para las predicciones de ambas tiendas y, por lo tanto, de acuerdo con esas metricas, estos errores de uno en uno son indistinguibles.
Esto se debe básicamente a que MSE trabaja con errores cuadrados absolutos, mientras que los errores relativos pueden ser más importantes para nosotros.
La preferencia de error relativo se puede expresar con el error de porcentaje cuadrático medio. Para cada objeto, el error absoluto se divide por el valor objetivo, dando un error relativo.
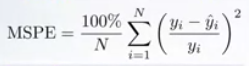
Entonces, MSPE puede ser pensado como versiones ponderadas de MSE. El peso de su muestra es inversamente proporcional a su cuadrado objetivo.
Esto significa que, el costo que pagamos por un error absoluto fijo, depende del valor objetivo y, a medida que aumenta, pagamos menos.
Dado que MSPE se considera como la versión ponderada de MSE, las predicciones constantes óptimas para MSPE resultan ser la media ponderada de los valores objetivo.
Error porcentual absoluto medio (MAPE)
La preferencia de error relativo también se puede expresar con el Error porcentual absoluto medio, MAPE. Para cada objeto, el error absoluto se divide por el valor objetivo, dando un error relativo. MAPE también puede ser pensado como versiones ponderadas de MAE.
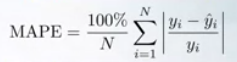
Para MAPE, el peso de su muestra es inversamente proporcional a su objetivo. Pero de manera similar a MSPE, el costo que pagamos por un error absoluto fijo depende del valor objetivo. Y a medida que aumenta el objetivo, pagamos menos.
Dado que MAPE se considera como la versión ponderada de MAE, las predicciones constantes óptimas para MAPE resultan ser la mediana ponderada de los valores objetivo.
Tenga en cuenta que si un valor atípico tuviera un valor muy, muy pequeño, MAPE estaría muy sesgado hacia él, ya que este valor atípico tendrá el peso más alto.
Error logarítmico cuadrático medio (RMSLE)
Es solo un RMSE calculado en escala logarítmica. De hecho, para calcularlo, tomamos un logaritmo de nuestras predicciones y los valores objetivo, y calculamos RMSE entre ellos.
Los objetivos generalmente no son negativos pero pueden ser iguales a 0, y el logaritmo de 0 no está definido. Es por eso que generalmente se agrega una constante a las predicciones y los objetivos antes de aplicar la operación logarítmica.
Esta constante también se puede elegir para que sea diferente a una dependiendo del problema.
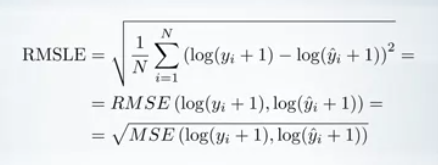
Por lo tanto, esta métrica se usa generalmente en la misma situación que MSPE y MAPE, ya que también conlleva errores relativos más que errores absolutos.
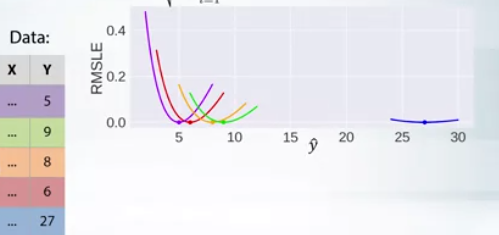
Tenga en cuenta la asimetría de las curvas de error . Desde la perspectiva de RMSLE, siempre es mejor predecir más de la misma cantidad menos que el objetivo. Por lo tanto, llegamos a la conclusión de que RMSLE penaliza una estimación poco predicha mayor que una estimación sobre pronosticada.
RMSLE se puede calcular sin la operación raíz, pero la versión rooteada se usa más ampliamente.
Ahora pasemos a la pregunta sobre la mejor constante. (Recuerde la conexión entre RMSLE y RMSE).
Primero, encontramos la mejor constante para RMSE en el espacio de registro, que será la media ponderada en el espacio de registro. Y, después, debemos regresar del espacio de registro al habitual con una transformación inversa.
Ejemplo

Observaciones:
- La constante óptima para RMSLE resulta ser 9.1, que es más alta que las constantes tanto para MAPE como para MSPE.
- MSE está bastante sesgada hacia el enorme valor de nuestro conjunto de datos, mientras que MAE está mucho menos sesgada.
- MSPE y MAPE están orientados hacia objetivos más pequeños porque asignan mayor peso al objeto con objetivos pequeños.
- RMSLE se considera con frecuencia como mejores métricas que MAPE, ya que está menos orientado hacia objetivos pequeños, pero funciona con errores relativos.
Que mensaje nos queda?
Te recomiendo que tomes un tiempo antes de comenzar un proyecto y pienses en la métrica apropiada, definitivamente le ayudará mucho.
Si te gusta este artículo también puedes volver a repasar la Parte 1 que abarca Machine Learning metricas de regresión MSE, RMSE, MAE y también recomendarte continuar con la parte 3 que trata un tema muy interesante como es la Seleccion Machine Learning metricas de clasificación
.
Gracias por leer y espero escuchar sus preguntas 🙂
Estén atentos y Feliz Machine Learning!.
PD Si quiere aprender más sobre el mundo del Machine Learning, también puede seguirme en Instagram o encuéntreme en linkedin . Me encantaría saber de ti.
